
【题目】已知,等边△ABC,点 E 在 BA 的延长线上,点 D 在 BC 上,且 ED=EC.
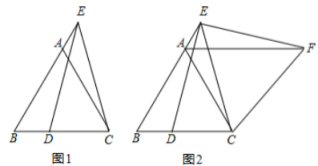
(1)如图 1,求证:AE=DB;
(2)如图 2,将△BCE 绕点 C 顺时针旋转 60°至△ACF(点 B、E 的对应点分别为点 A、F),连接 EF.在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对线段长度之差等于 AB 的长.
【答案】(1)见解析;(2)![]() ;
;![]() ;
;![]() ;
;![]() .
.
【解析】
(1)在BA上截取BF=BD,连接DF,根据等边三角形的性质可得∠BAC=∠B=∠ACB=60°,从而证出△BDF为等边三角形,然后利用AAS证出△CEA≌△EDF,从而得出AE=DF,即可证出结论;
(2)根据图形、全等三角形的性质、旋转的性质和等量代换即可得出结论.
解:(1)在BA上截取BF=BD,连接DF
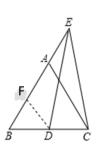
∵△ABC是等边三角形
∴∠BAC=∠B=∠ACB=60°,
∵BF=BD,
∴△BDF为等边三角形
∴BD=DF,∠BFD=∠FDB=60°
∴∠BFD=∠BAC
∴FD∥AC
∴∠EAC=∠DFE
∵ED=EC
∴∠EDC=∠ECD
∵∠EDC+∠EDF=180°-∠FDB=120°,∠ECD+∠CEA=180°-∠B=120°
∴∠CEA=∠EDF
在△CEA和△EDF中
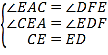
∴△CEA≌△EDF
∴AE=DF
∴AE=DB
(2)由图可知:![]()
∵AE=DB
∴![]()
由旋转的性质可得:BE=AF
∴![]()
∴![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象过A(﹣3,m),B(5,m),C(0,m+2),D(﹣1,y1),E(﹣5,y2),F(6,y3),则函数值y1,y2,y3的大小关系是( )
A.y2<y3<y1B.y3<y1<y2C.y2<y1<y3D.y1<y3<y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△A1B1C1中,A1B1=4,A1C1=5,B1C1=7.点A2,B2,C2分别是边B1C1,A1C1,A1B1的中点;点A3,B3,C3分别是边B2C2,A2C2,A2B2的中点;…以此类推,则第2020个三角形的周长是_____.
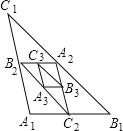
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小元步行从家去火车站,走到 6 分钟时,以同样的速度回家取物品,然后从家乘出租车赶往火车站,结果比预计步行时间提前了3 分钟.小元离家路程S(米)与时间t(分钟)之间的函数图象如图,从家到火车站路程是( )

A.1300 米B.1400 米C.1600 米D.1500 米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,规定把一个点先绕原点逆时针旋转45°,再作出旋转后的点关于原点的对称点,这称为一次变换,已知点A的坐标为(﹣1,0),则点A经过连续2018次这样的变换得到的点A2018的坐标是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=a(x﹣m)2﹣m+1(a、m为常数且a<0),下列结论:
①这个函数图象的顶点始终在直线y=﹣x+1上;
②a(x-1)(x+3)=﹣1有两个根x1和x2,且x1<x2,则﹣3<x1<x2<1;
③点A(x1,y1)与点B(x2,y2)在函数图象上,若x1<x2,x1+x2≥2m,则y1≤y2;
④当﹣1<x<2时,y随x的增大而增大,则m的取值范围为m≥2.
其中正确结论的序号是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() (m>0)与x轴的交点为A,B.
(m>0)与x轴的交点为A,B.
(1)求抛物线的顶点坐标;
(2)横、纵坐标都是整数的点叫做整点.
①当m=1时,求线段AB上整点的个数;
②若抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)恰有6个整点,结合函数的图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,若干个半径为3个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为每秒3个单位长度,点在弧线上的速度为每秒π个单位长度,则2020秒时,点P的坐标是( )
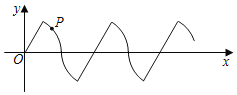
A.(2020,0)B.(3030,0)C.( 3030,![]() )D.(3030,﹣
)D.(3030,﹣![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com