
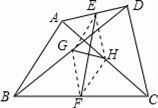
.如图,在四边形ABCD中,E、F分别是AD、BC的中点,G、H分别是BD、AC的中点,当AB、CD满足条件 时,有EF⊥GH.


AB=CD
【考点】中点四边形.
【分析】连接EG、GF、FH、HE,根据三角形中位线定理得到EG∥AB,EG=
 AB,GF∥CD,GF=
AB,GF∥CD,GF=
 CD,FH∥AB,FH=
CD,FH∥AB,FH=
 AB,EH∥CD,EH=
AB,EH∥CD,EH=
 CD,得到平行四边形EGFH,根据菱形的判定和性质证明结论.
CD,得到平行四边形EGFH,根据菱形的判定和性质证明结论.
【解答】解:当AB=CD时,EF⊥GH.
利用:连接EG、GF、FH、HE,
∵E、G分别是AD、BD的中点,
∴EG∥AB,EG=
 AB,
AB,
同理GF∥CD,GF=
 CD,FH∥AB,FH=
CD,FH∥AB,FH=
 AB,EH∥CD,EH=
AB,EH∥CD,EH=
 CD,
CD,
∴EG∥FH,EG=FH,
∴四边形EGFH是平行四边形,
当AB=CD时,EG=EH,
∴四边形EGFH是菱形,
∴EF⊥GH.
故答案为:AB=CD.



科目:初中数学 来源: 题型:
如图, AD为△ABC的中线,BE为△ABD的中线.
(1)∠ABE=15°,∠BAD=36°,求∠BED的度数;
(2) 作出△BED中DE边上的高,垂足为H;
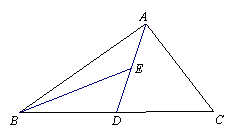 (3) 若△ABC面积为20,过点C作CF//AD交BA的延长线于点F,求△BCF的面积。(友情提示:两条平行线间的距离处处相等.)
(3) 若△ABC面积为20,过点C作CF//AD交BA的延长线于点F,求△BCF的面积。(友情提示:两条平行线间的距离处处相等.)
查看答案和解析>>
科目:初中数学 来源: 题型:
小明手里有6张完全一样的卡片,其中4张正面画上记号“A”,另外2张卡片被画上记号“B”,先将其背面朝上洗匀,让小东从中随机抽取2张卡片,则他抽出的两张均有“A”记号的卡片的概率等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图.
根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图;
(2)求扇形统计图中m的值和“E”组对应的圆心角度数;
(3)请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数.


查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,直线y=﹣3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,点D在双曲线
 (k≠0)上.将正方形沿x轴负方向平移a个单位长度后,点C恰好落在该双曲线上,则a的值是( )
(k≠0)上.将正方形沿x轴负方向平移a个单位长度后,点C恰好落在该双曲线上,则a的值是( )


A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
.下列命题中,真命题是( )
A.四边相等的四边形是正方形
B.对角线相等的菱形是正方形
C.正方形的两条对角线相等,但不互相垂直平分
D.矩形、菱形、正方形都具有“对角线相等”的性质
查看答案和解析>>
科目:初中数学 来源: 题型:
某学校为了解本校学生课外阅读的情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成统计表.已知该校全体学生人数为1200人,由此可以估计每周课外阅读时间在1~2(不含1)小时的学生有 人.
| 每周课外阅读时间(小时) | 0~1 | 1~2 (不含1) | 2~3 (不含2) | 超过3 |
| 人 数 | 7 | 10 | 14 | 19 |
查看答案和解析>>
科目:初中数学 来源: 题型:
实验室里,水平桌面上有甲、乙两个圆柱形容器(容器足够高),底面半径之比为1∶2,用一个管子在甲、乙两个容器的15厘米高度处连通(即管子底端离容器底15厘米).已知只有乙容器中有水,水位高2厘米,如图所示.现同时向甲、乙两个容器注水,平均每分钟注入乙容器的水量是注入甲容器水量的k倍.开始注水1分钟,甲容器的水位上升a厘米,且比乙容器的水位低1厘米.其中a,k均为正整数,当甲、乙两个容器的水位都到达连通管子的位置时,停止注水.甲容器的水位有2次比
乙容器的水位高1厘米,设注水时间为t分钟.
(1)求k的值(用含a的代数式表示).
(2)当甲容器的水位第一次比乙容器的水位高1厘米时,求t的值.
(3)当甲容器的水位第二次比乙容器的水位高1厘米时,求a,k,t的值.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com