练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，直线l是一条河，A，B两地相距5km，A，B两地到l的距离分别为3km、6km，欲在l上的某点M处修建一个水泵站，向A，B两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则铺设的管道最短的是（ ）
    A.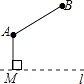
    B.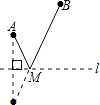
    C.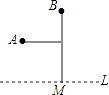
    D.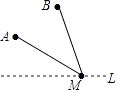

    【答案】B
    【解析】解：根据最短路线问题，B选项图形方案符合．
    故选B．
    【考点精析】解答此题的关键在于理解垂线段最短的相关知识，掌握连接直线外一点与直线上各点的所有线段中，垂线段最短；现实生活中开沟引水，牵牛喝水都是“垂线段最短”性质的应用，以及对轴对称-最短路线问题的理解，了解已知起点结点，求最短路径；与确定起点相反，已知终点结点，求最短路径；已知起点和终点，求两结点之间的最短路径；求图中所有最短路径．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，∠ABC与∠ACB的平分线交于点F，过点F作DE∥BC交AB于点D，交AC于点E，那么下列结论：
    ①△BDF和△CEF都是等腰三角形；
    ②DE=BD+CE；
    ③△ADE的周长等于AB与AC的和；
    ④BF=CF．
    其中正确的有（ ）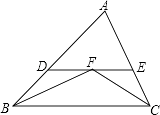

    A.①②③
    B.①②③④
    C.①②
    D.①

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解方程：3x＝x（x+5）﹣8

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某服装店用4500元购进一批衬衫，很快售完，服装店老板又用2100元购进第二批该款式的衬衫，进货量是第一次的一半，但进价每件比第一批降低了10元．

    （1）这两次各购进这种衬衫多少件？

    （2）若第一批衬衫的售价是200元/件，老板想让这两批衬衫售完后的总利润不低于1950元，则第二批衬衫每件至少要售多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解答
    （1）如图（1），已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D，E．
    证明：DE=BD+CE．

    （2）如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D，A，E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．

    （3）拓展与应用：如图（3），D，E是D，A，E三点所在直线m上的两动点（D，A，E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD，CE，若∠BDA=∠AEC=∠BAC，试判断△DEF的形状．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了解某社区居民的用电情况，随机对该社区10户居民进行调查，下表是这10户居民2017年4月份用电量的调查结果：

    居 民（户）

    1

    2

    3

    4

    月用电量（度/户）

    30

    42

    50

    51

    那么关于这10户居民月用电量（单位：度），下列说法错误的是（　　）

    A. 中位数是50 B. 方差是42 C. 众数是51 D. 极差是21

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】请根据图中提供的信息，回答下列问题：

    （1）一个暖瓶与一个水杯分别是多少元？（只填写结果）

    一个暖瓶　 　元；一个水杯　 　元．

    （2）甲、乙两家商场同时出售同样的暖瓶和水杯，为了迎接新年，两家商场都在搞促销活动，甲商场规定：这两种商品都打九折；乙商场规定：买一个暖瓶赠送二个水杯，单独买水杯不优惠．若某单位想要买4个暖瓶和15个水杯，请问选择哪家商场购买更合算，并说明理由．

    （3）若必须买5个暖瓶，则当买多少个水杯时到两家商城一样合算．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解答
    （1）如图，在四边形ABCD中，AB=AD，∠B=∠D=90°，E，F分别是边BC，CD上的点，且∠EAF= ∠BAD．
    求证：EF=BE+FD；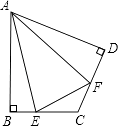

    （2）如图，在四边形ABCD中，AB=AD，∠B+∠D=180°，E，F分别是边BC，CD上的点，且∠EAF= ∠BAD，（1）中的结论是否仍然成立？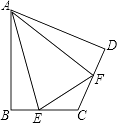

    （3）如图，在四边形ABCD中，AB=AD，∠B+∠ADC=180°，E、F分别是边BC、CD延长线上的点，且∠EAF= ∠BAD，（1）中的结论是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明．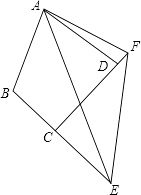

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点O为△ABC的外心，若∠A=80°，则∠BOC的度数为（ ）
    A.40°
    B.80°
    C.120°
    D.160°

    查看答案和解析>>

    同步练习册答案