
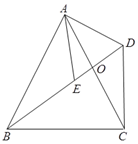
【题目】如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且AE=AD,∠EAD=∠BAC.
⑴ 求证:∠ABD=∠ACD;
⑵ 若∠ACB=65°,求∠BDC的度数.
【答案】(1)见解析;(2) 50°
【解析】(1)关键全等三角形的判定与性质证明即可;(2)利用三角形的外角性质和三角形的内角和解答即可.
详解:⑴∵ ∠BAC=∠EAD
∴ ∠BAC-∠EAC=∠EAD-∠EAC
即:∠BAE=∠CA,
在△ABE和△ACD中
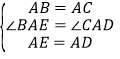
∴ △ABE≌△ACD,
∴ ∠ABD=∠ACD,
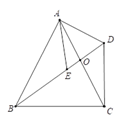
⑵∵ ∠BOC是△ABO和△DCO的外角
∴ ∠BOC=∠ABD+∠BAC,∠BOC=∠ACD+∠BDC
∴ ∠ABD+∠BAC=∠ACD+∠BDC
∵ ∠ABD=∠ACD
∴ ∠BAC=∠BDC,
∵ ∠ACB=65°,AB=AC
∴ ∠ABC=∠ACB=65°,
∴ ∠BAC=180°-∠ABC-∠ACB=180°-65°-65°=50°,
∴ ∠BDC=∠BAC=50°


科目:初中数学 来源: 题型:
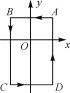
【题目】如图,在平面直角坐标系中:A(1,1),B(-1,1),C(-1,-2),D(1,-2),现把一条长为2 018个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→B→C→D→A→…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线y= ![]() x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+4ax+b经过A.C两点,且与x轴交于另一点B.
x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+4ax+b经过A.C两点,且与x轴交于另一点B.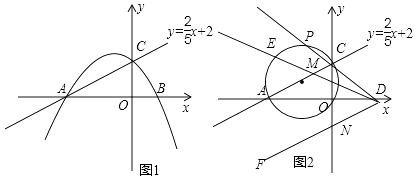
(1)求抛物线的解析式;
(2)若点Q在抛物线上,且△AQC与△BQC面积相等,求点Q的坐标;
(3)如图2,P为△AOC外接圆上弧ACO的中点,直线PC交x轴于点D,∠EDF=∠ACO,当∠EDF绕点D旋转时,DE交直线AC于点M,DF交y轴负半轴于点N.请你探究:CN﹣CM的值是否发生变化?若不变,求出其值;若变化,求出变化范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
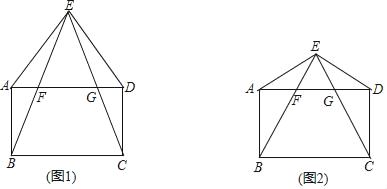
【题目】已知:点E为矩形ABCD外一点,连接AE,DE,且AE=DE,连接EB,EC分别与AD相交于点F,G.
(1)如图1,求证:∠ABE=∠DCE;
(2)如图2,若△BCE是等边三角形,且AE=AB,在不添加任何辅助线的情况下,请直接写出图2中四对全等的钝角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个多位自然数的任意两个相邻数位上,右边数位上的数总比左边数位上数大1,那么我们把这样的自然数叫做“相连数”.例如:234,4567,56789,…都是“相连数”.
(1)请直接写出最大的两位“相连数”与最小的三位“相连数”,并求它们的差.
(2)若某个“相连数”恰好等于其个位数的469倍,求这个“相连数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某项针对18﹣35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,m≥15时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,制作图表如下: 18﹣35岁青年人日均发微博条数统计表
m | 频数 | 百分数 |
A级(0≤m<5) | 90 | 0.3 |
B级(5≤m<10) | 120 | a |
C级(10≤m<15) | b | 0.2 |
D级(m≥15) | 30 | 0.1 |
请你根据以上信息解答下列问题:
(1)求a,b;
(2)补全频数分布直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践探究
在数学实践课上,小明提出了这样的问题:分数![]() 可以写为小数形式,即0.
可以写为小数形式,即0.![]() 反过来,无限循环小数0.
反过来,无限循环小数0. ![]() 写成分数形式即为
写成分数形式即为![]() .那么无限循环小数0.
.那么无限循环小数0. ![]() 应怎样化为分数呢?
应怎样化为分数呢?
小明是这样思考的:
在学习解一元一次方程时,当变形到ax=b(a≠0)形式后,通过系数化1,两边同时除以a,得到方程的解x=![]() ,
,![]() 就是分数形式.
就是分数形式.
设0. ![]() =x,即x=0.777…,又10x=7.77…,这里x、0.777…、10x、7.77…存在着关系,根据这一关系我就可以找到相等关系,列出方程.
=x,即x=0.777…,又10x=7.77…,这里x、0.777…、10x、7.77…存在着关系,根据这一关系我就可以找到相等关系,列出方程.
请你阅读小明的思考过程,把无限循环小数0. ![]() 化为分数的过程写出来.
化为分数的过程写出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级共有8个班,241名同学,历史老师为了了解新中考模式下该校八年级学生选修历史学科的意向,请小红,小亮,小军三位同学分别进行抽样调查.三位同学调查结果反馈如下:
小红、小亮和小军三人中,你认为哪位同学的调查结果较好地反映了该校八年级同学选修历史的意向,请说出理由,并由此估计全年级有意向选修历史的同学的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com