
【题目】如图,在平面直角坐标系中一次函数 ![]() 的图象分别交x、y轴于点A、B,与一次函数y=x的图象交于第一象限内的点C.
的图象分别交x、y轴于点A、B,与一次函数y=x的图象交于第一象限内的点C.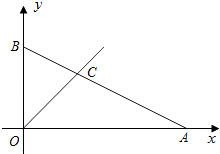
(1)分别求出A、B、C、的坐标;
(2)求出△AOC的面积.
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①S△ABF=S△ADF;②S△CDF=4S△CEF;③S△ADF=2S△CEF;④S△ADF=2S△CDF , 其中正确的是( ) 
A.①③
B.②③
C.①④
D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AB=4,AD=2,点P是边AB上的一个动点(不与点A、点B重合),点Q在边AD上,将△CBP和△QAP分别沿PC、PQ折叠,使B点与E点重合,A点与F点重合,且P、E、F三点共线.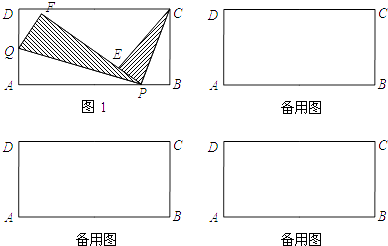
(1)若点E平分线段PF,则此时AQ的长为多少?
(2)若线段CE与线段QF所在的平行直线之间的距离为2,则此时AP的长为多少?
(3)在“线段CE”、“线段QF”、“点A”这三者中,是否存在两个在同一条直线上的情况?若存在,求出此时AP的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=kx+b与坐标轴分别交于点A(0,8)、B(8,0),动点 C从原点O出发沿OA方向以每秒1个单位长度向点A运动,动点D从点B出发沿BO方向以每秒1个单位长度向点O运动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动,设运动时间为t 秒.
(1)直接写出直线的解析式:;
(2)若E点的坐标为(﹣2,0),当△OCE的面积为5 时.
①求t的值;
②探索:在y轴上是否存在点P,使△PCD的面积等于△CED的面积?若存在,请求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一条长为40cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于52cm2 , 那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于48cm2吗?若能,求出两段铁丝的长度;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为了了解员工每人所创年利润情况,公司从各部抽取部分员工对每年所创年利润情况进行统计,并绘制如图1,图2统计图. 
(1)将图补充完整;
(2)本次共抽取员工人,每人所创年利润的众数是 , 平均数是;
(3)若每人创造年利润10万元及(含10万元)以上位优秀员工,在公司1200员工中有多少可以评为优秀员工?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com