
【题目】某公司为了了解员工每人所创年利润情况,公司从各部抽取部分员工对每年所创年利润情况进行统计,并绘制如图1,图2统计图. 
(1)将图补充完整;
(2)本次共抽取员工人,每人所创年利润的众数是 , 平均数是;
(3)若每人创造年利润10万元及(含10万元)以上位优秀员工,在公司1200员工中有多少可以评为优秀员工?
【答案】
(1)解:3万元的员工的百分比为:1﹣36%﹣20%﹣12%﹣24%=8%,
抽取员工总数为:4÷8%=50(人)
5万元的员工人数为:50×24%=12(人)
8万元的员工人数为:50×36%=18(人)
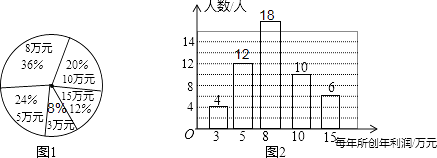
(2)50;8万元;8.12万元
(3)解:1200× ![]() =384(人)
=384(人)
答:在公司1200员工中有384人可以评为优秀员工
【解析】解:(2)抽取员工总数为:4÷8%=50(人)
每人所创年利润的众数是 8万元,
平均数是: ![]() (3×4+5×12+8×18+10×10+15×6)=8.12万元
(3×4+5×12+8×18+10×10+15×6)=8.12万元
故答案为:50,8万元,8.12万元.
(1)求出3万元的员工的百分比,5万元的员工人数及8万元的员工人数,再据数据制图.(2)利用3万元的员工除以它的百分比就是抽取员工总数,利用定义求出众数及平均数.(3)优秀员工=公司员工×10万元及(含10万元)以上优秀员工的百分比.


科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中xOy中,抛物线y=ax2﹣2ax﹣3a(a<0)与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:y=kx+b与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
(1)求A、B两点的坐标及抛物线的对称轴;
(2)求直线l的函数表达式(其中k、b用含a的式子表示);
(3)点E是直线l上方的抛物线上的动点,若△ACE的面积的最大值为 ![]() ,求a的值;
,求a的值;
(4)设P是抛物线对称轴上的一点,点Q在抛物线上,以点A、D、P、Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中一次函数 ![]() 的图象分别交x、y轴于点A、B,与一次函数y=x的图象交于第一象限内的点C.
的图象分别交x、y轴于点A、B,与一次函数y=x的图象交于第一象限内的点C.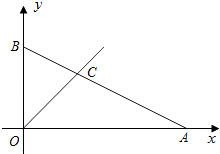
(1)分别求出A、B、C、的坐标;
(2)求出△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠DAC=∠ACB,要使四边形ABCD成为平行四边形,则应增加的条件不能是( ) 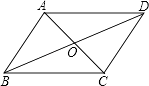
A.AD=BC
B.OA=OC
C.AB=CD
D.∠ABC+∠BCD=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=6,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则△PEF和△PGH的面积和等于 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+9﹣b2(b为常数)经过坐标原点O,且与x轴交于另一点E.其顶点M在第一象限.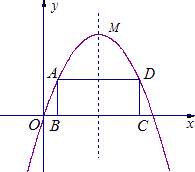
(1)求该抛物线所对应的函数关系式;
(2)设点A是该抛物线上位于x轴上方,且在其对称轴左侧的一个动点;过点A作x轴的平行线交该抛物线于另一点D,再作AB⊥x轴于点B,DC⊥x轴于点C.
①当线段AB、BC的长都是整数个单位长度时,求矩形ABCD的周长;
②求矩形ABCD的周长的最大值,并写出此时点A的坐标;
③当矩形ABCD的周长取得最大值时,它的面积是否也同时取得最大值?请判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为6cm的正方形ABCD中,点E、F、G、H分别从点A、B、C、D同时出发,均以1cm/s的速度向点B、C、D、A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,当运动时间为s时,四边形EFGH的面积最小,其最小值是cm2 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com