
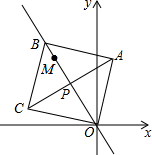
 如图,点M(-3,4),点P从O点出发,沿射线OM方向1个单位/秒匀速运动,运动的过程中以P为对称中心,O为一个顶点作正方形OABC,当正方形面积为128时,点A坐标是( )
如图,点M(-3,4),点P从O点出发,沿射线OM方向1个单位/秒匀速运动,运动的过程中以P为对称中心,O为一个顶点作正方形OABC,当正方形面积为128时,点A坐标是( )| A. | ($\frac{3}{2}$,$\frac{65}{6}$) | B. | ($\sqrt{7}$,11) | C. | (2,2$\sqrt{31}$) | D. | ($\frac{8}{5}$,$\frac{56}{5}$) |
分析 作AD⊥x轴于D,CE⊥x轴于E,根据M的坐标求得直线OM的斜率-$\frac{4}{3}$,进一步得出直线AC的斜率为$\frac{3}{4}$,通过证得△COE≌△OAD,得出CE=OD,OE=AD,所以设A(a,b),则C(-b,a),然后根据待定系数法求得直线AC的斜率为$\frac{b-a}{a+b}$,从而得出$\frac{b-a}{a+b}$=$\frac{3}{4}$,整理得b=7a,然后在RT△AOD中,根据勾股定理得出(7a)2+a2=128,解得a=$\frac{8}{5}$,b=$\frac{56}{5}$.
解答 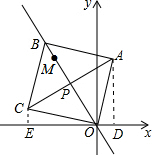 解:作AD⊥x轴于D,CE⊥x轴于E,
解:作AD⊥x轴于D,CE⊥x轴于E,
设直线OM的解析式为y=kx,
∵点M(-3,4),
∴4=-3k,
∴k=-$\frac{4}{3}$,
∵四边形ABCO是正方形,
∴直线AC⊥直线OM,
∴直线AC的斜率为$\frac{3}{4}$,
∵四边形ABCO是正方形,
∴OA=OC,∠AOC=90°,
∴∠AOD+∠COE=90°,
∵∠AOD+∠OAD=90°
∴∠COE=∠OAD,
在△COE和△OAD中,
$\left\{\begin{array}{l}{∠COE=∠OAD}\\{∠CEO=∠ODA=90°}\\{OC=OA}\end{array}\right.$
∴△COE≌△OAD(AAS),
∴CE=OD,OE=AD,
设A(a,b),则C(-b,a),
设直线AC的解析式为y=mx+n,
∴$\left\{\begin{array}{l}{am+n=b①}\\{-bm+n=a②}\end{array}\right.$
解得m=$\frac{b-a}{a+b}$,
∴$\frac{b-a}{a+b}$=$\frac{3}{4}$,
整理得,b=7a,
∵正方形面积为128,
∴OA2=128,
在RT△AOD中,AD2+OD2=OA2,即(7a)2+a2=128,
解得,a=$\frac{8}{5}$,
∴b=7a=7×$\frac{8}{5}$=$\frac{56}{5}$,
∴A($\frac{8}{5}$,$\frac{56}{5}$),
故选D.
点评 本题是一次函数的综合题,考查了待定系数法求一次函数的解析式,正方形的性质,全等三角形的判定和性质,勾股定理的应用等,根据直线AC的斜率列出方程是本题的关键.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题
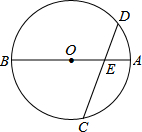 如图,AB为⊙O的直径,弦CD与AB相交于点E,且OE=DE,试确定$\widehat{BC}$与$\widehat{AD}$之间的数量关系.
如图,AB为⊙O的直径,弦CD与AB相交于点E,且OE=DE,试确定$\widehat{BC}$与$\widehat{AD}$之间的数量关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
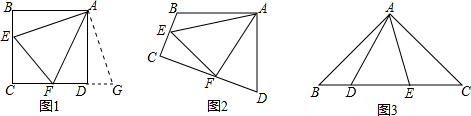
 如图,若要建一个长方形鸡场,鸡场的一边靠墙,墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米,围成长方形的鸡场除门之外四周不能有空隙.求:
如图,若要建一个长方形鸡场,鸡场的一边靠墙,墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米,围成长方形的鸡场除门之外四周不能有空隙.求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
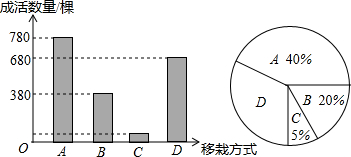 某园林部门为扩大绿化面积,进行了大量树木的移栽,他们选择A、B、C、D四种方式对2000棵树进行移栽,并分别统计四种移栽方式的成活情况,旨在提高来年移栽树木的成活率,通过计算制成下表以及两个统计图,经确认图甲有误,其它正确.
某园林部门为扩大绿化面积,进行了大量树木的移栽,他们选择A、B、C、D四种方式对2000棵树进行移栽,并分别统计四种移栽方式的成活情况,旨在提高来年移栽树木的成活率,通过计算制成下表以及两个统计图,经确认图甲有误,其它正确. | 移栽方式 | A | B | C | D |
| 成活率 | 97.5% | 95% | 60% | 90% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
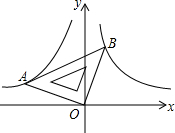 如图,一块等腰直角三角板AOB的直角顶点O与坐标原点生命,点B、A分别在第一、二象限,反比例函数y=$\frac{{k}_{1}}{x}$、y=$\frac{{k}_{2}}{x}$的图象分别经过点A、B,若点A的坐标是(-3,1),分别求出k1,k2的值.
如图,一块等腰直角三角板AOB的直角顶点O与坐标原点生命,点B、A分别在第一、二象限,反比例函数y=$\frac{{k}_{1}}{x}$、y=$\frac{{k}_{2}}{x}$的图象分别经过点A、B,若点A的坐标是(-3,1),分别求出k1,k2的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com