
【题目】在△ABC中,D为BC上一点,连接AD,过点B作BE垂直于CA的延长线于点E,BE与DA的延长线相交于点F.
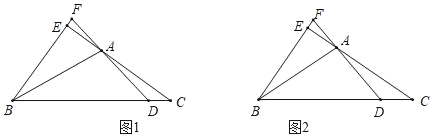
(1)如图1,若AB平分∠CBE,∠ADB=30°,AE=3,AC=7,求CD的长;
(2)如图2,若AB=AC,∠ADB=45°,求证;BC=![]() DF.
DF.
【答案】(1)CD=2![]() ﹣3
﹣3![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)作AH⊥BC于H.解直角三角形求出DH,CH即可解决问题.
(2)作FM⊥BC于M.AN⊥BC于N,设AE交FM于点O.证明△FMD是等腰直角三角形,△FMB≌△BNA(AAS)即可解决问题.
解:(1)作AH⊥BC于H.
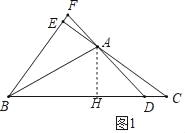
∵AB平分∠EBC,AE⊥BF,AH⊥BC,
∴AE=AH=3,
在Rt△AHD中,∵∠ADH=30°,
∴AD=2AH=6,DH=![]() =3
=3![]() ,
,
在Rt△ACH中,CH=![]() =2
=2![]() ,
,
∴CD=CH﹣DH=2![]() ﹣3
﹣3![]() .
.
(2)如图,作FM⊥BC于M.AN⊥BC于N,设AE交FM于点O.
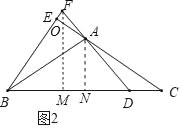
∵CE⊥BF,FM⊥BC,
∴∠OEF=∠OMC,∵∠EOF=∠MOC,
∴∠OFE=∠C,
∵AB=AC,
∴∠C=∠ABC,
∴∠OFE=∠B,
∵∠FDM=∠MFD=45°,
∴FM=DM,DF=![]() FM,
FM,
∵∠BFA=45°+∠BFM,∠BAF=∠ABC+∠ADB=45°+∠ABD,
∴∠BFA=∠BAF,
∴BF=BA,
∵∠BFA=∠ABN,BF=BA,∠FMB=∠ANB=90°,
∴△FMB≌△BNA(AAS),
∴FM=BN,
∴BC=2BN=2FM=![]() DF.
DF.


科目:初中数学 来源: 题型:
【题目】意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的边长值构造正方形,再分别依次从左到右取2个、3个、4个、5个…正方形拼成如上长方形,若按此规律继续作长方形,则序号为⑦的长方形周长是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
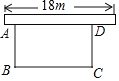
【题目】为响应荆州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)若矩形空地的面积为160m2,求x的值;
(3)若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.
甲 | 乙 | 丙 | |
单价(元/棵) | 14 | 16 | 28 |
合理用地(m2/棵) | 0.4 | 1 | 0.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 交
交![]() 轴于点
轴于点![]() 、
、![]() ,交
,交![]() 轴于点
轴于点![]() ,在
,在![]() 轴上有一点
轴上有一点![]() ,连接
,连接![]() .
.
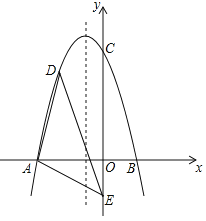
(1)求二次函数的表达式;
(2)若点![]() 为抛物线在
为抛物线在![]() 轴负半轴上方的一个动点,求
轴负半轴上方的一个动点,求![]() 面积的最大值;
面积的最大值;
(3)抛物线对称轴上是否存在点![]() ,使
,使![]() 为等腰三角形,若存在,请直接写出所有
为等腰三角形,若存在,请直接写出所有![]() 点的坐标,若不存在请说明理由.
点的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大课间到了,小明和小欢两人打算从教室匀速跑到600米外的操场做课间操,刚出发时小明就发现鞋带松了,停下来系鞋带,小欢则直接前往操场,小明系好鞋带后立即沿同一路开始追赶小欢,小明在途中追上小欢后继续前行,小明到达操场时课间操还没有开始,于是小明站在操场等待,小欢继续前往操场,设小明和小欢两人想距s(米),小欢行走的时间为t(分钟),s关于t的函数的部分图象如图所示,当两人第三次相距60米时,小明离操场还有_____米.
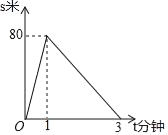
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在线段![]() 上有一点
上有一点![]() ,在
,在![]() 的同侧作等腰
的同侧作等腰![]() 和等腰
和等腰![]() ,且
,且![]() ,
,![]() ,
,![]() ,直线
,直线![]() 与线段
与线段![]() ,线段
,线段![]() 分别交于点
分别交于点![]() ,对于下列结论:①
,对于下列结论:①![]() ∽
∽![]() ;②
;②![]() ∽
∽![]() ;③
;③![]() ;④若
;④若![]() ,则
,则![]() .其中正确的是( )
.其中正确的是( )
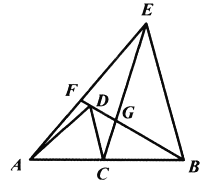
A. ①②③④B. ①②③C. ①③④D. ①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点P(﹣2,1)关于y轴的对称点P′,点T(t,0)是x轴上的一个动点,当△P′TO是等腰三角形时,t的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小明家住在30米高的A楼里,小丽家住在B楼里,B楼坐落在A楼的正北面,已知当地冬至中午12时太阳光线与水平面的夹角为30°.
(1)如果A、B两楼相距16![]() 米,那么A楼落在B楼上的影子有多长?
米,那么A楼落在B楼上的影子有多长?
(2)如果A楼的影子刚好不落在B楼上,那么两楼的距离应是多少米?(结果保留根号)
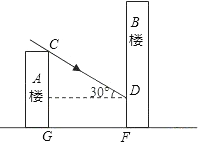
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com