
 如图,在六边形ABCDEF中,AF∥CD,AB∥DE,BC∥EF,且∠A=110°,∠B=82°,试求六边形其余各角的度数.
如图,在六边形ABCDEF中,AF∥CD,AB∥DE,BC∥EF,且∠A=110°,∠B=82°,试求六边形其余各角的度数. 分析 分别延长AF、DE交于点G,延长AB、DC交于点H,可证得四边形AGDH为平行四边形,可得∠D=∠A.分别延长FA、CB交于点M,延长FE、CD交于点N,
四边形FMCN为平行四边形,可得∠AFN=∠MCN,∠M+∠AFN=180°,所以∠AFN=∠MCN=180°-∠M=180°-12°=168°,再利用六边形的内角和,即可求出∠DEF.
解答 解:如图,分别延长AF、DE交于点G,延长AB、DC交于点H;分别延长FA、CB交于点M,延长FE、CD交于点N,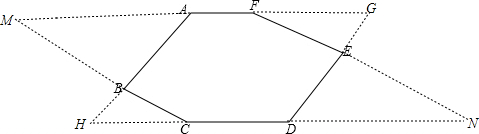
∵AF∥CD,AB∥DE,
∴四边形AGDH为平行四边形,
∴∠FAB=∠CDE=110°,
∵∠FAB=110°,
∴∠MAB=180°-∠FAB=70°,
∵∠ABC=82°,
∴∠M=∠ABC-∠MAB=82°-70°=12°,
∵AF∥CD,BC∥EF,
∴四边形FMCN为平行四边形,
∴∠AFN=∠MCN,∠M+∠AFN=180°,
∴∠AFN=∠MCN=180°-∠M=180°-12°=168°,
六边形的内角和为:(6-2)×180°=720°,
∴∠DEF=720°-∠FAB-∠ABC-∠BCD-∠CDE-AFE=82°.
点评 本题主要考查平行四边形的判定和性质,掌握两组对边分别平行的四边形为平行四边形是解题的关键.


科目:初中数学 来源: 题型:解答题
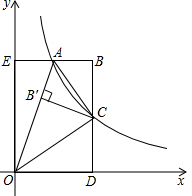 在平面直角坐标系中,点(0.5,4)在双曲线y=$\frac{m}{x}$上.
在平面直角坐标系中,点(0.5,4)在双曲线y=$\frac{m}{x}$上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
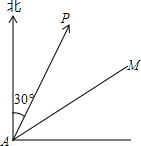 如图所示,小岛P的周围20$\sqrt{2}$海里内有暗礁,某渔船沿北偏东60°的AM方向航行,在A处测得小岛P的方向为北偏东30°,且距A处40海里,该渔船若不改变航向,有无触礁的可能?若有可能触礁,则该渔船在A处应再向北偏东至少偏离多大角度才能脱险?
如图所示,小岛P的周围20$\sqrt{2}$海里内有暗礁,某渔船沿北偏东60°的AM方向航行,在A处测得小岛P的方向为北偏东30°,且距A处40海里,该渔船若不改变航向,有无触礁的可能?若有可能触礁,则该渔船在A处应再向北偏东至少偏离多大角度才能脱险?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
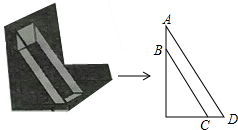 如图,某时刻太阳光从窗户射入室内,与地面的夹角∠ADC为60°,窗户的高AB在阳光下的投影为CD,此时测得CD的长为0.8m,求窗户的高.(精确到0.1m,参考数据:$\sqrt{2}$=1.414,$\sqrt{3}$=1.732)
如图,某时刻太阳光从窗户射入室内,与地面的夹角∠ADC为60°,窗户的高AB在阳光下的投影为CD,此时测得CD的长为0.8m,求窗户的高.(精确到0.1m,参考数据:$\sqrt{2}$=1.414,$\sqrt{3}$=1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
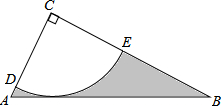 如图,Rt△ABC中,∠C=90°,AC=$\sqrt{5}$,tanB=$\frac{1}{2}$,半径为2的⊙C,分别交AC,BC于点D,E,得到$\widehat{DE}$.
如图,Rt△ABC中,∠C=90°,AC=$\sqrt{5}$,tanB=$\frac{1}{2}$,半径为2的⊙C,分别交AC,BC于点D,E,得到$\widehat{DE}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com