
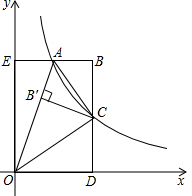
 在平面直角坐标系中,点(0.5,4)在双曲线y=$\frac{m}{x}$上.
在平面直角坐标系中,点(0.5,4)在双曲线y=$\frac{m}{x}$上.分析 (1)把点(0.5,4)代入y=$\frac{m}{x}$,求出m的值,即可得出结果;
(2)①由折叠的性质得出:△△AB′C≌△ABC,得出∠AB′C=∠B,CB′=CB,再由角平分线的性质得出CB′=CD,得出CB=CD即可;
②由C是BD的中点,得出△OCD的面积=$\frac{1}{4}$矩形ODBE的面积,再根据双曲线的解析式求出△OCD的面积=△AOE的面积=1,四边形OABC的面积=矩形ODBE的面积-△OCD的面积-△AOE的面积,即可得出结果.
解答 解:(1)把点(0.5,4)代入y=$\frac{m}{x}$得:m=0.5×4=2,
∴双曲线的解析式为:y=$\frac{2}{x}$;
(2)①证明:根据题意得:△△AB′C≌△ABC,
∴∠AB′C=∠B,CB′=CB,
∵四边形ODBE是矩形,
∴∠ODC=∠B=90°,OD=BE,OE=BD,
∴∠AB′C=∠B=90°,
∵OC平分∠AOD,
∴CB′=CD,
∴CB=CD,
即点C是BD的中点;
②∵四边形ODBE是矩形,C是BD的中点,
∴△OCD的面积=$\frac{1}{4}$矩形ODBE的面积,
∵y=$\frac{2}{x}$,
∴△OCD的面积=△AOE的面积=$\frac{2}{2}$=1,
∴矩形ODBE的面积=4,
∴四边形OABC的面积=矩形ODBE的面积-△OCD的面积-△AOE的面积=4-1-1=2.
点评 本题是反比例函数综合题目,考查了反比例函数解析式的求法、折叠的性质、全等三角形的性质、角平分线的性质以及面积的计算等知识;本题综合性强,有一定难度,熟练掌握矩形的性质和反比例函数,并能进行推理计算是解决问题的关键.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$+3$\sqrt{2}$=5$\sqrt{5}$ | B. | -a8÷a4=-a2 | C. | (3a2)3=27a6 | D. | (a2-b)2=a4-b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 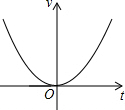 | B. |  | C. | 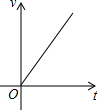 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com