
【题目】如图,已知直线AB经过x轴上的点A(2,0),且与抛物线相交于B、C两点,已知B点坐标为(1,1) .
(1)求直线和抛物线的解析式;
(2)如果D为抛物线上一点,使得△AOD与△OBC的面积相等,求D点坐标。

【答案】(1)y=x2;(2)D点坐标为(![]() ,3)或(﹣
,3)或(﹣![]() ,3).
,3).
【解析】
(1)将A、B两点坐标代入y=kx+b中,可求直线解析式,将B点坐标代入y=ax2中,可求抛物线解析式;
(2)联立直线与抛物线解析式,可求C点坐标,用S△OBC=S△OCA-S△OBA,可求△OAD的面积,又已知OA,可求D点的纵坐标.
(1)设直线AB所表示的函数解析式为y=kx+b,
∵它过点A(2,0)和点B(1,1),
∴![]()
解得![]()
∴直线AB所表示的函数解析式为y=﹣x+2,
设抛物线的解析式为y=ax2
∵抛物线y=ax2过点B(1,1),
∴a×12=1,
解得a=1,
∴抛物线所表示的函数解析式为y=x2;
(2)解方程组![]()
得![]()
![]()
∵B点坐标为(1,1)
∴C点坐标为(﹣2,4)
∴OA=2,![]()
![]()
∴S△OBC=S△OAC﹣S△OAB=4﹣1=3,
设D点的纵坐标为yD,
则![]()
∴yD=3y=3代入y=x2,
得x=±![]() ,
,
∴D点坐标为(![]() ,3)或(﹣
,3)或(﹣![]() ,3).
,3).


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
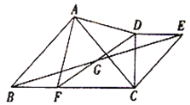
【题目】已知:如图,线段AB和射线BM交于点B.
(1)利用尺规完成以下作图,并保留作图痕迹(不写作法)
①在射线BM上作一点C,使AC=AB;
②作∠ABM 的角平分线交AC于D点;
③在射线CM上作一点E,使CE=CD,连接DE.

(2)在(1)所作的图形中,猜想线段BD与DE的数量关系,并证明之.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④AE=EC,其中正确的是________(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 与
与![]() 有公共顶点
有公共顶点![]() (顶点均按逆时针排列),
(顶点均按逆时针排列),![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() 并延长交直线
并延长交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)如图,当![]() 时,
时,
求证:①![]() ;
;
②![]() 是等腰直角三角形.
是等腰直角三角形.
(2)当![]() 时,画出相应的图形(画一个即可),并直接指出
时,画出相应的图形(画一个即可),并直接指出![]() 是何种特殊三角形.
是何种特殊三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解方程:
(1)25 y 2- 16 = 0; (2)y 2+ 2 y-99=0;
(3)3x 2 + 2x -3=0; (4)(2x + 1)2 =3(2x + 1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地相距60km,甲从A地去B地,乙从B地去A地,图中![]() 、
、![]() 分别表示甲、乙两人到B地的距离y(km)与甲出发时间x(h)的函数关系图象.
分别表示甲、乙两人到B地的距离y(km)与甲出发时间x(h)的函数关系图象.
(1)根据图象,求乙的行驶速度.
(2)解释交点A的实际意义.
(3)求甲出发多少时间,两人之间恰好相距5km?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张三同学投掷一枚骰子两次,两次所投掷的点数分别用字母m、n表示
(1)求使关于x的方程x2﹣mx+2n=0有实数根的概率;
(2)求使关于x的方程mx2+nx+1=0有两个相等实根的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com