
【题目】如图,△ABC是边长为5的等边三角形,点D,E分别在BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的的延长线于点F,若BD=2,则DF等于( )
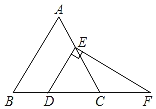
A.7B.6C.5D.4
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,则下列结论正确的有_____.
①abc>0
②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3
③2a+b=0
④当x>0时,y随x的增大而减小

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,己知
中,己知![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上沿
上沿![]() 到
到![]() 的方向以每秒
的方向以每秒![]() 的速度运动(不与点
的速度运动(不与点![]() ,
,![]() 重合),点
重合),点![]() 在
在![]() 上,且满足
上,且满足![]() ,设点
,设点![]() 运动时间为
运动时间为![]() 秒,当
秒,当![]() 是等腰三角形时,
是等腰三角形时,![]() ________.
________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料,解决问题.
例题:若m2 +2mn+2n2-6n+9=0,求m和n的值.
解:∵ m2+2mn+2n2- 6n+9=0,
∴m2 +2mn+n2+n2-6n+9=0,
∴(m+n)2 +(n-3)2=0,
∴m+n=0, n-3=0,
∴m=-3, n=3.
问题: (1)若2x2 +4x-2xy+y2 +4=0,求xy的值;
(2)已知a, b, c是△ABC的三边长,且满足a2+b2=10a+8b-41,求c的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,对任意一个正整数n都可以进行这样的分解:n=p![]() q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p
q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p![]() q是n的最佳分解,并规定:F(n)=
q是n的最佳分解,并规定:F(n)=![]() ,例如12可以分解为1
,例如12可以分解为1![]() 12,2
12,2![]() 6或3
6或3![]() 4,因为12-1>6-2>4-3,所以3
4,因为12-1>6-2>4-3,所以3![]() 4是最佳分解,所以F(n)=
4是最佳分解,所以F(n)=![]() 。
。
(1)如果一个正整数![]() 是另外一个正整数b的平方,我们称正整数a是完全平方数,求证:对任意一个完全平方数m,总有F(m)=1
是另外一个正整数b的平方,我们称正整数a是完全平方数,求证:对任意一个完全平方数m,总有F(m)=1
(2)如果一个两位正整数t,t=10x+y (1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们就称这个数t为“吉祥数”,求所有“吉祥数”中F(t)的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)6a(a﹣2)﹣(2﹣3a)2;
(2)(2x2﹣3y)(2x2+3y)﹣2x(﹣3x3);
(3)先化简,再求值:[2(x﹣y)]2﹣(12x3y2﹣18x2y3)÷(3xy2),其中x=﹣3,y=﹣![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠BAD=100°,∠B=∠D=90°,在BC、CD上分别找一个点M、N,使△AMN的周长最小,则∠AMN+∠ANM的度数为( )

A.130°B.120°C.160°D.100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】CD是线段AB的垂直平分线,则∠CAD=∠CBD.请说明理由.

解:∵CD是线段AB的垂直平分线(已知),
∴AC=______,______=BD(______)
在△ADC和______中,
______=BC,
AD=______,
CD=______(______),
∴______≌______(______ ).
∴∠CAD=∠CBD (全等三角形的对应角相等).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=2![]() x2的图象如图所示,点O为坐标原点,点A在y轴的正半轴上,点B、C在函数图象上,四边形OBAC为菱形,且∠OBA=120°,则点C的坐标为______.
x2的图象如图所示,点O为坐标原点,点A在y轴的正半轴上,点B、C在函数图象上,四边形OBAC为菱形,且∠OBA=120°,则点C的坐标为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com