
【题目】已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,则下列结论正确的有_____.
①abc>0
②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3
③2a+b=0
④当x>0时,y随x的增大而减小

【答案】②③
【解析】由函数图象可得抛物线开口向下,得到a<0,又对称轴在y轴右侧,可得b>0,根据抛物线与y轴的交点在y轴正半轴,得到c>0,进而得到abc<0,结论①错误;由抛物线与x轴的交点为(3,0)及对称轴为x=1,利用对称性得到抛物线与x轴另一个交点为(﹣1,0),进而得到方程ax2+bx+c=0的两根分别为﹣1和3,结论②正确;由抛物线的对称轴为x=1,利用对称轴公式得到2a+b=0,结论③正确;由抛物线的对称轴为直线x=1,得到对称轴右边y随x的增大而减小,对称轴左边y随x的增大而增大,故x大于0小于1时,y随x的增大而增大,结论④错误.
∵抛物线开口向下,∴a<0,
∵对称轴在y轴右侧,∴![]() >0,∴b>0,
>0,∴b>0,
∵抛物线与y轴的交点在y轴正半轴,∴c>0,
∴abc<0,故①错误;
∵抛物线与x轴的一个交点为(3,0),又对称轴为直线x=1,
∴抛物线与x轴的另一个交点为(﹣1,0),
∴方程ax2+bx+c=0的两根是x1=﹣1,x2=3,故②正确;
∵对称轴为直线x=1,∴![]() =1,即2a+b=0,故③正确;
=1,即2a+b=0,故③正确;
∵由函数图象可得:当0<x<1时,y随x的增大而增大;
当x>1时,y随x的增大而减小,故④错误;
故答案为②③.


科目:初中数学 来源: 题型:
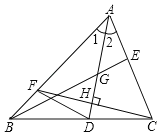
【题目】如图所示,在△ABC中,AD是∠BAC的平分线,G是AD上一点,且AG=DG,连接BG并延长BG交AC于E,又过C作AD的垂线交AD于H,交AB为F,则下列说法正确的是_____(填序号).
①D是BC的中点;②∠CDA>∠2;③BE是△ABC的边AC上的中线;
④CH为△ACD的边AD上的高;⑤△AFC为等腰三角形;
⑥连接DF,若CF=6,AD=8,则四边形ACDF的面积为24.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线x=-4与x轴交于点E,一开口向上的抛物线过原点交线段OE于点A,交直线x=-4于点B,过B且平行于x轴的直线与抛物线交于点C,直线OC交直线AB于D,且AD:BD=1:3.

(1)求点A的坐标;
(2)若△OBC是等腰三角形,求此抛物线的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
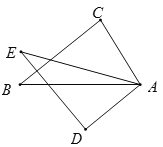
【题目】如图,已知,![]() ,AC=AD.给出下列条件: ①AB=AE;②BC=ED;③
,AC=AD.给出下列条件: ①AB=AE;②BC=ED;③![]() ;④
;④ ![]() .其中能使
.其中能使![]() 的条件为__________ (注:把你认为正确的答案序号都填上).
的条件为__________ (注:把你认为正确的答案序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D’的坐标是( )
A.(2,10)B.(-2,0)C.(2,10)或(-2,0)D.(10,2)或(-5,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
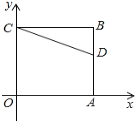
【题目】已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为![]() 、
、![]() ,点D是OA的中点,点P在BC边上运动,当
,点D是OA的中点,点P在BC边上运动,当![]() 是等腰三角形时,点Р的坐标为_______________.
是等腰三角形时,点Р的坐标为_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为5的等边三角形,点D,E分别在BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的的延长线于点F,若BD=2,则DF等于( )
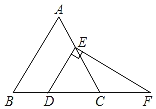
A.7B.6C.5D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com