
【题目】希望中学计划从荣威公司买A、B两种型号的小黑板,经治谈,购买一块A型小黑板比购买一块B型小黑板多用20元,且购买5块A型小黑板和购买4块B型小黑板共需820元.
![]() 求购买一块A型小黑板,一块B型小黑板各需要多少元?
求购买一块A型小黑板,一块B型小黑板各需要多少元?
![]() 根据希望中学实际情况,需从荣威公司买A,B两种型号的小黑板共60块,要求购买A、B两种型号的小黑板的总费用不超过5240元,并且购买A型小黑板的数量应大于购买A、B两种型号的小黑板总数量的
根据希望中学实际情况,需从荣威公司买A,B两种型号的小黑板共60块,要求购买A、B两种型号的小黑板的总费用不超过5240元,并且购买A型小黑板的数量应大于购买A、B两种型号的小黑板总数量的![]() ,请你通过计算,求出希望中学从荣威公司买A、B两种型号的小黑板有哪几种方案?并说明哪种方案更节约资金?
,请你通过计算,求出希望中学从荣威公司买A、B两种型号的小黑板有哪几种方案?并说明哪种方案更节约资金?
【答案】(1) A型小黑板单价为100元,B型小黑板单价为80元;(2) 有两种购买方案:方案一:A型21块,B型39块,共需费用5220元方案二:A型22块,B型38块,共需费用5240元.故方案一更省钱.
【解析】
(1)设购买一块A型小黑板需x元,则购买一块B型小黑板需(x-20)元,根据等量关系:购买5块A型小黑板的费用+购买4块B型小黑板的费用=820列出方程,解方程即可求得所求答案;
(2)设购买A型小黑板m块,则购买B型小黑板(60-m)块,根据不等关系:购买两种小黑板的费用不超过5240元和购买A型小黑板的数量大于购买两种小黑板总量的三分之一列出不等式组,解不等式组求得其整数解即可得到所求答案.
![]() 设购买一块A型小黑板需要x元,一块B型为
设购买一块A型小黑板需要x元,一块B型为![]() 元,
元,
![]() ,
,
解得:![]() ,
,
∴![]() ,
,
购买一块A型小黑板需100元,购买一块B型小黑板需80元;
![]() 设购买A型小黑板m块,则购买B型小黑板
设购买A型小黑板m块,则购买B型小黑板![]() 块,根据题意得:
块,根据题意得:
 ,
,
解得:![]() ,
,
∵m为整数,
∴m的值为21或22.
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
∴有两种购买方案:
方案一:A型21块,B型39块,共需费用100×21+80×39=5220(元);
方案二:A型22块,B型38块,共需费用100×22+80×38=5240(元).
故方案一更省钱.


科目:初中数学 来源: 题型:
【题目】如图,点A为函数y= ![]() (x>0)图象上一点,连结OA,交函数y=
(x>0)图象上一点,连结OA,交函数y= ![]() (x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为 .
(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E.

(1)判断四边形ACED的形状,并说明理由;
(2)若BD=8cm,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,直线![]() ,E为AB、CD间的一点,连接EA、EC.
,E为AB、CD间的一点,连接EA、EC.
![]() 如图
如图![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
![]() 如图
如图![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
![]() 如图
如图![]() ,若
,若![]() ,
,![]() ,则
,则![]() ,
,![]() 与
与![]() 之间有何等量关系
之间有何等量关系![]() 并简要说明.
并简要说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年某企业按餐厨垃圾处理费25元/ 吨、建筑垃圾处理费16元/ 吨的收费标准,共支付餐厨和建筑垃圾处理费5200元.从2018年元月起,收费标准上调为:餐厨垃圾处理费100元/ 吨,建筑垃圾处理费30元/ 吨.若该企业2018年处理的这两种垃圾数量与2017年相比没有变化,就要多支付垃圾处理费8800元.
(1)该企业2017年处理的餐厨垃圾和建筑垃圾各多少吨?
(2)该企业计划2018年将上述两种垃圾处理总量减少到240吨,且建筑垃圾处理量不超过餐厨垃圾处理量的3倍,则2018年该企业最少需要支付餐厨垃圾处理费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
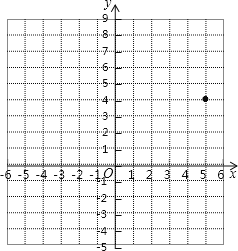
【题目】在平面直角坐标系中,A、B、C三点的坐标分别为![]() 、
、![]() 、
、![]() .
.
![]() 画出
画出![]() ,并求
,并求![]() 的面积;
的面积;
![]() 在
在![]() 中,点C经过平移后的对应点为
中,点C经过平移后的对应点为![]() ,将
,将![]() 作同样的平移得到
作同样的平移得到![]() ,画出平移后的
,画出平移后的![]() ,并写出点
,并写出点![]() ,
,![]() 的坐标;
的坐标;
![]() 已知点
已知点![]() 为
为![]() 内一点,将点P向右平移4个单位后,再向下平移6个单位得到点
内一点,将点P向右平移4个单位后,再向下平移6个单位得到点![]() ,则
,则![]() ______,
______,![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2ax+1与x轴仅有一个公共点A,经过点A的直线交该抛物线于点B,交y轴于点C,且点C是线段AB的中点.
(1)求这条抛物线对应的函数解析式;
(2)求直线AB对应的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校同学五一假期参加社团活动的情况,抽查了100名同学,统计它们假期参加社团活动的时间,绘成频数分布直方图(如图),则参加社团活动时间的中位数所在的范围是( )
A.4﹣6小时
B.6﹣8小时
C.8﹣10小时
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y1=kx+b的图象与反比例函数![]() 的图象交于A、B两点, 且点A的坐标为(-2,3),点B的纵坐标是-2,求:
的图象交于A、B两点, 且点A的坐标为(-2,3),点B的纵坐标是-2,求:
(1)一次函数与反比例函数的解析式;
(2)利用图像指出,当![]() 为何值时有
为何值时有![]() >
>![]() ;当
;当![]() 为何值时有
为何值时有![]() <
<![]()
(3)利用图像指出,当![]() >3时
>3时![]() 的取值范围。
的取值范围。

【答案】见解析
【解析】试题分析:(1)把A点坐标代入反比例函数解析式求出m的值,把B点的纵坐标代入反比例函数解析式求出B点的横坐标,再把A、B两点的坐标代入一次函数解析式求出k、b的值即可;
(2)根据A、B的横坐标,结合图象即可得出答案;
(3)求出x=3时y2的值,然后结合图象即可得出y2的取值范围.
试题解析:
解:(1)∵A(-2,3)在反比例函数y2=![]() 的图象上,
的图象上,
∴m=-2×3
=-6,
即反比例函数的解析式为y2=![]() .
.
当y2=-2时,x=3,
即B(3,-2),
把A(-2,3),B(3,-2)代入y=kx+b得:
![]() ,
,
解得: ![]() ,
,
即一次函数的解析式为y=-x+1;
(2)结合图象可得y1>y2时对应的图象在点A的左侧和y轴与点B之间,
即x<-2或0<x<3;
同理y1<y2时对应的图象在点A与y轴之间和点B的右侧,
即-2<x<0或x>3;
(3)当x=3时,y2=-2,
当x>3时反比例函数对应的图象在点B的右侧部分,
对应的函数值-2<y2<0.
点睛:本题考查了一次函数与反比例函数的交点问题,用待定系数法求一次函数的解析式等知识点,主要考查学生的计算能力和观察图形的能力,用了数形结合思想.
【题型】解答题
【结束】
26
【题目】如图,四边形ABCD是平行四边形,点A(1,0),B(4,1),C(4,4).反比例函数![]() (x>0)的图像经过点D,点P是一次函数y=ax+4-4a(a
(x>0)的图像经过点D,点P是一次函数y=ax+4-4a(a![]() 0)的图像与该反比例函数图像的一个公共点.
0)的图像与该反比例函数图像的一个公共点.
(1)求反比例函数的表达式;
(2)一次函数y=ax+4-4a(a![]() 0)的图像恒过一定点,直接写出这个定点的坐标.
0)的图像恒过一定点,直接写出这个定点的坐标.
(3)对于一次函数y=ax+4-4a(a![]() 0),当y随x的增大而减小时,确定点P的横坐标的取值范围.(不必写出过程)
0),当y随x的增大而减小时,确定点P的横坐标的取值范围.(不必写出过程)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com