
【题目】如图,河边有 A,B 两个村庄,A 村距河边 10m,B 村距河边 30m,两村平行于河边方 向的水平距离为 30m,现要在河边建一抽水站 E,需铺设管道抽水到 A 村和 B 村.

(1)要使铺设管道的长度最短,请作图找出水站 E 的位置(不写作法)
(2)若铺设管道每米需要 500 元,则最低费用为多少?
【答案】(1)见解析(2)25000元
【解析】
(1)先求出点A关于河流的对称点A′,然后连接A′B,与河流的交点E即为所求作的抽水站的位置.利用勾股定理求出A′B即为铺设管道的最短距离.
(2)运用费用=米数×每米的钱数.
(1)如图所示,抽水站修在点E处才能使所需的管道最短.

先求出点A关于河流的对称点A′,然后连接A′B,与河流的交点E即为所求作的抽水站的位置.
作BC垂直于河,A′C平行河.
∵两村的水平距离为30米,
∴A′C=30米.
∵A村距河边10米,B村距河边30米,
∴BC=10+30=40(米).
∴A′B=![]() =50(米).
=50(米).
(2)最低费用为:50×500=25000(元).


科目:初中数学 来源: 题型:
【题目】已知:线段![]() 厘米.
厘米.
(1)如图一,点![]() 沿线段
沿线段![]() 自
自![]() 点向
点向![]() 点以4厘米/分的速度运动,同时点
点以4厘米/分的速度运动,同时点![]() 沿线段
沿线段![]() 自
自![]() 点向
点向![]() 点以6厘米/分的速度运动.求:①几分钟后
点以6厘米/分的速度运动.求:①几分钟后![]() 两点相遇? ②几分钟后
两点相遇? ②几分钟后![]() 两点相距20厘米?
两点相距20厘米?
(2)如图二,![]() 厘米,
厘米,![]() ,现将点
,现将点![]() 绕着点
绕着点![]() 以20度/分的速度顺时针旋转一周后停止,同时点
以20度/分的速度顺时针旋转一周后停止,同时点![]() 沿直线
沿直线![]() 自
自![]() 点向
点向![]() 点运动,假若
点运动,假若![]() 两点也能相遇,求点
两点也能相遇,求点![]() 的速度.
的速度.
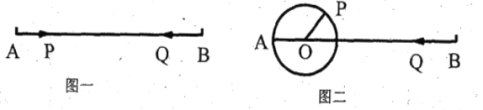
查看答案和解析>>
科目:初中数学 来源: 题型:
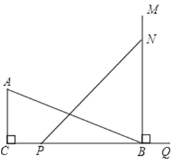
【题目】如图,CA⊥BC,垂足为C,AC=2Cm,BC=6cm,射线BM⊥BQ,垂足为B,动点P从C点出发以1cm/s的速度沿射线CQ运动,点N为射线BM上一动点,满足PN=AB,随着P点运动而运动,当点P运动_______秒时,△BCA与点P、N、B为顶点的三角形全等.(2个全等三角形不重合)
查看答案和解析>>
科目:初中数学 来源: 题型:
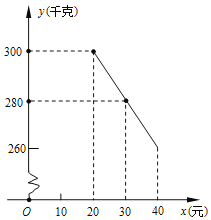
【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x 的函数关系图象.
(1)求y与x的函数关系式;
(2)直接写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图4,点A,B,C在数轴上表示的数分别是1,![]() ,
,![]() ,点E到点B,C的距离相等,点P从点A出发,向左运动,速度是每秒0.3个单位长度.设运动的时间是t秒.
,点E到点B,C的距离相等,点P从点A出发,向左运动,速度是每秒0.3个单位长度.设运动的时间是t秒.
(1)点E表示的数是________;
(2)在t=3,t=4这两个时刻,使点P更接近原点O的时间是哪一个?
(3)若点P分别t=8,t=p两个不同的时刻,到点E的距离相等,求p的值;
(4)设点M在数轴上表示的数是m,点N在数轴上表示的数是n,式子________的值可以体现点M和点N之间的距离,这个式子的值越小,两个点的距离越近.
查看答案和解析>>
科目:初中数学 来源: 题型:
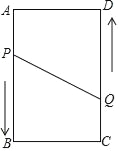
【题目】如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2cm/s的速度向D移动.
(1)P、Q两点从出发开始到几秒时,四边形APQD为长方形?
(2)P、Q两点从出发开始到几秒时?四边形PBCQ的面积为33cm2;
(3)P、Q两点从出发开始到几秒时?点P和点Q的距离是10cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
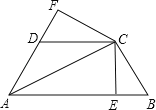
【题目】如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
(1)求证:△BCE≌△DCF;
(2)若AB=15,AD=7,BC=5,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简再求值:
(1)![]() ,其中
,其中![]()
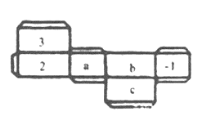
(2)如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
①填空:![]() _________,
_________,![]() _________
_________![]() _________;
_________;
②先化简,再求值:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长都是1,每个小正方形的顶点叫做格点.网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1 (要求A与A1,B与B1,C与C1相对应);
(2)求△ABC的面积;
(3)在直线l上找一点P,使得△PAC的周长最小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com