
【题目】如图,点D,E在△ABC的边BC上,连接AD,AE.下面有三个等式:①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,相构成以下三个命题:命题Ⅰ“如果①②成立,那么③成立”; 命题Ⅱ“如果①③成立,那么②成立”;命题Ⅲ“如果②③成立,那么①成立”. 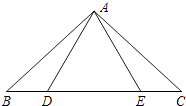
(1)以上三个命题是真命题的为(直接作答);
(2)请选择一个真命题进行证明(先写出所选命题,然后证明).
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中,点A(﹣3,﹣1)、B(﹣2,﹣4)、C(﹣6,﹣5),以原点为位似中心将△ABC缩小,位似比为1:2,则点B的对应点的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在平面直角坐标系中,直线l与y轴相交于点A(0,m)其中m<0,与x轴相交于点B(4,0).抛物线y=ax2+bx(a>0)的顶点为F,它与直线l相交于点C,其对称轴分别与直线l和x轴相交于点D和点E.
(1)设a=![]() ,m=﹣2时,
,m=﹣2时,
①求出点C、点D的坐标;
②抛物线y=ax2+bx上是否存在点G,使得以G、C、D、F四点为顶点的四边形为平行四边形?如果存在,求出点G的坐标;如果不存在,请说明理由.
(2)当以F、C、D为顶点的三角形与△BED相似且满足三角形FAC的面积与三角形FBC面积之比为1:3时,求抛物线的函数表达式.
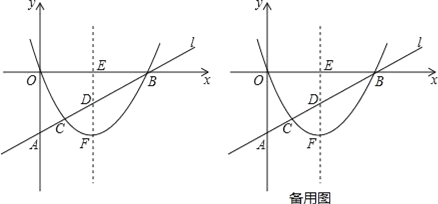
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:甲、乙两车分别从相距300(km)的M、N两地同时出发相向而行,其中甲到达N地后立即返回,图1、图2分别是它们离各自出发地的距离y(km)与行驶时间x(h)之间的函数图象.
(1)试求线段AB所对应的函数关系式,并写出自变量的取值范围;
(2)当它们行驶到与各自出发地距离相等时,用了4.5(h),求乙车的速度;
(3)在(2)的条件下,求它们在行驶的过程中相遇的时间.
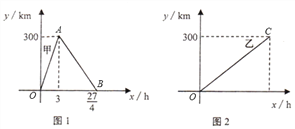
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有![]() 个选项,第二道单选题有
个选项,第二道单选题有![]() 个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(![]() )如果小明第一题不使用“求助”,那么小明答对第一道题的概率是__________.
)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是__________.
(![]() )如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明通关的概率.
)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明通关的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )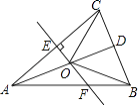
A.1对
B.2对
C.3对
D.4对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com