
【题目】如图,在△ABC中,∠ ACB=90°,点D在BC边上,且BD=BC,过点B作CD的垂线交AC于点O,以O为圆心,OC为半径画圆.
(1)求证:AB是⊙O的切线;
(2)若AB=10,AD=2,求⊙O的半径.
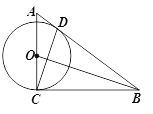
【答案】(1)证明见解析;(2)⊙O的半径为![]()
【解析】(1)连接OD,先证△DBO≌△CBO,再证∠ODB=∠OCB=90°即可;(2)在Rt△ABC中由勾股定理建立方程,从而求出⊙O的半径.
(1)证明:连接OD
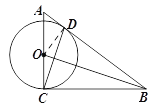
∵BD=BC,BO⊥CD
∴∠DBO=∠CBO
∵BD=BC,∠DBO=∠CBO,OB=OB
∴△DBO≌△CBO
∴OD=OC,∠ODB=∠OCB=90°
∴AB是⊙O的切线
(2)∵AB=10,AD=2,∴BC=BD=AB-AD=8
在Rt△ABC中, ![]()
设⊙O的半径为r,则OD=OC=r,AO=AC-OC=6-r
在Rt△ADO中,∵AD2+OD2=AO2
∴22+r 2=(6-r)2
解之得![]() ,即⊙O的半径为
,即⊙O的半径为![]()
“点睛”本题考查了圆的切线的判定以及勾股定理的运用,解题关键是在直角三角形中利用勾股定理列出方程.


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
【题目】如图,点A、O、B在同一条直线上,∠AOC=∠BOD,OE是∠BOC的平分线.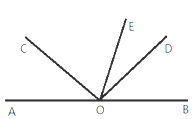
(1)若∠AOC=46°,求∠DOE的度数;
(2)若∠DOE=30°,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①长度相等的弧是等弧;②任意三点确定一个圆;③相等的圆心角所对的弦相等;④平分弦的直径垂直于弦,并且平分弦所对的两条弧;其中真命题共有( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在相同的条件下各射靶10次,每次命中的环数如下:
甲:9,7,8,9,7,6,10,10,6,8;
乙:7,8,8,9,7,8,9,8,10,6
(1)分别计算甲、乙两组数据的方差;
(2)根据计算结果比较两人的射击水平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,①9的平方根是3;②9的平方根是±3;③﹣0.027没有立方根;④﹣3是27的负的立方根;⑤一个数的平方根等于它的算术平方根,则这个数是0;⑥ ![]() 的平方根是±4,其中正确的有( )
的平方根是±4,其中正确的有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了推动球类运动的普及,成立多个球类运动社团,为此,学生会采取抽样调查的方法,从足球、乒乓球、篮球、排球四个项目调查了若干名学生的兴趣爱好(要求每位同学只能选择其中一种自己喜欢的球类运动),并将调查结果绘制成了如下条形统计图和扇形统计图(不完整).请你根据图中提供的信息,解答下列问题: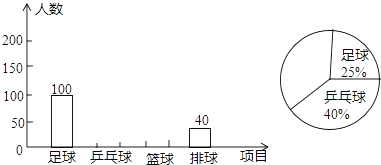
(1)本次抽样调查,共调查了名学生;
(2)请将条形统计图和扇形统计图补充完整;
(3)若该学校共有学生1800人,根据以上数据分析,试估计选择排球运动的同学约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=﹣2x+4的图象如图,图象与x轴交于点A,与y轴交于点B.
(1)求A、B两点坐标.
(2)求图象与坐标轴所围成的三角形的面积是多少.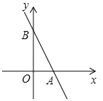
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com