
【题目】如图,一个长方形运动场被分隔成ABABC共5个区,A区是边长为a m的正方形,C区是4个边长为b m的小正方形组成的正方形.
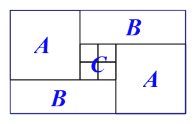
(1)列式表示每个B区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果a=40 m,b=20 m,求整个长方形运动场的面积.
【答案】(1) (a+2b+a—2b)×2,4a ;(2)4a +2(a+2b)+2(a—2b),8a;(3) 4800 m2
【解析】
(1)利用图形得出区域B的长和宽,即可得出答案;
(2)利用图形得出整个长方形的长和宽,即可得出答案;
(3)借助(2)求出的长和宽,利用面积公式计算即可得出答案.
解:(1)由图可知:B区长方形的长是(a+b)m,宽是(a-b)m
则B区长方形的周长=(a+2b+a-2b)×2=4a(m)
(2)由图可知:整个长方形的长是(a+b+a)m,宽是(a+a-b)m
则整个长方形的周长=4a+2(a+2b)+2(a-2b)=8a (m)
(3)S=(2a-2b)×﹙2a+2b﹚=4 a2- 4b2 (m2)
当a=40,b=20时,原式=4 ×402- 4×202=4800 (m2)
答:整个长方形运动场的面积为4800 m2


科目:初中数学 来源: 题型:
【题目】如图1是边长为![]() 的正方形薄铁片,小明将其四角各剪去一个相同的小正方形(图中阴影部分)后,发现剩余的部分能折成一个无盖的长方体盒子,图2为盒子的示意图(铁片的厚度忽略不计).
的正方形薄铁片,小明将其四角各剪去一个相同的小正方形(图中阴影部分)后,发现剩余的部分能折成一个无盖的长方体盒子,图2为盒子的示意图(铁片的厚度忽略不计).
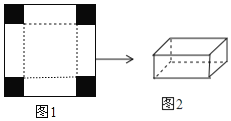
(1)设剪去的小正方形的边长为![]() ,折成的长方体盒子的容积为
,折成的长方体盒子的容积为![]() , 用只含字母
, 用只含字母![]() 的式子表示这个盒子的高为________
的式子表示这个盒子的高为________![]() ,底面积为________
,底面积为________![]() ,盒子的容积
,盒子的容积![]() 为________
为________![]() ;
;
(2)为探究盒子的体积与剪去的小正方形的边长![]() 之间的关系,小明列表
之间的关系,小明列表
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|
| _______ |
|
|
| _______ |
|
|
请将表中数据补充完整,并根据表格中的数据写出当![]() 的值逐渐增大时,
的值逐渐增大时,![]() 的值如何变化?
的值如何变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强环境保护意识,争创“文明卫生城市”,某企业对职工进行了依次“生产和居住环境满意度”的调查,按年龄分组,得到下面的各组人数统计表:
各组人数统计表
组号 | 年龄分组 | 频数(人) | 频率 |
第一组 | 20≤x<25 | 50 | 0.05 |
第二组 | 25≤x<30 | a | 0.35 |
第三组 | 35≤x<35 | 300 | 0.3 |
第四组 | 35≤x<40 | 200 | b |
第五组 | 40≤x≤45 | 100 | 0.1 |
(1)求本次调查的样本容量及表中的a、b的值;
(2)调查结果得到对生产和居住环境满意的人数的频率分布直方图如图,政策规定:本次调查满意人数超过调查人数的一半,则称调查结果为满意.如果第一组满意人数为36,请问此次调查结果是否满意;并指出第五组满意人数的百分比;
(3)从第二张和第四组对生产和居住环境满意的职工中分别抽取3人和2人作义务宣传员,在这5人中随机抽取2人介绍经验,求第二组和第四组恰好各有1人被抽中介绍经验的概率.
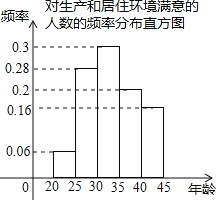
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算与化简
(1)-18+21+(-13)
(2)-81÷![]() ×
×![]() ÷(-16)
÷(-16)
(3)(![]() +
+![]() -
-![]() )×(-24)
)×(-24)
(4)-22-![]() ×[4-(-3)2]
×[4-(-3)2]
(5)化简:5(3x2y-xy2)-4(-xy2+2x2y)
(6)先化简,再求值:-![]() x+2(x-
x+2(x-![]() y2) - (-
y2) - (-![]() x+
x+![]() y2);其中x=2,y=
y2);其中x=2,y=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是小明记录的今年雨季一周河水的水位变化情况(上周末的水位达到警戒水位).
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位变化/米 | +0.20 | +0.81 | ﹣0.35 | +0.03 | +0.28 | ﹣0.36 | ﹣0.01 |
注:正号表示水位比前一天上升,负号表示水位比前一天下降.
(1)本周哪一天河流的水位最高?哪一天河流的水位最低?它们位于警戒水位之上还是之下?与警戒水位的距离分别是多少米?
(2)与上周相比,本周末河流水位是上升了还是下降了?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图甲是小明设计的带菱形图案的花边作品.该作品由形如图乙的矩形图案拼接而成(不重叠、无缝隙).图乙中![]() ,EF=4cm,上下两个阴影三角形的面积之和为54cm2,其内部菱形由两组距离相等的平行线交叉得到,则该菱形的周长为_____cm.
,EF=4cm,上下两个阴影三角形的面积之和为54cm2,其内部菱形由两组距离相等的平行线交叉得到,则该菱形的周长为_____cm.
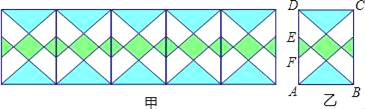
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知多项式(a2﹣16)x2+(a+4)x+4a是关于x的一次多项式,且常数项为b,a、b分别对应着数轴上的A、B两点.
(1)a= ,b= ;
(2)若点P从点A出发,以每秒3个单位长度的速度向x轴正半轴运动,求运动时间为多少时,点P到点A的距离是点P到点B的距离的3倍;
(3)数轴上还有一点C表示的数为40,若点P和点Q同时从点A和点B出发,分别以每秒4个单位长度和每秒2个单位长度的速度向C点运动,P点到达C点后,再立刻以同样的速度返回,运动到终点A,求运动多少秒时,P、Q两点之间的距离为6.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com