
【题目】我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段AB的最小覆盖圆就是以线段AB为直径的圆.
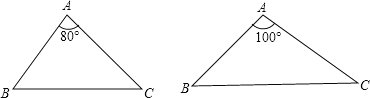
(1)请分别作出下图中两个三角形的最小覆盖圆(要求用尺规作图,保留作图痕迹,不写作法);
(2)探究三角形的最小覆盖圆有何规律?请写出你所得到的结论(不要求证明).
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC是等边三角形,点D、E分别在边BC、AC上,∠ADE=60°.
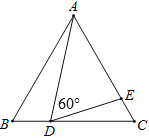
(1)求证:△ABD∽△DCE;
(2)如果AB=3,EC=![]() ,求DC的长.
,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
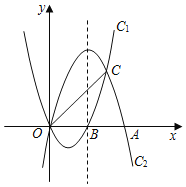
【题目】如图,抛物线C1:y=x2﹣2x与抛物线C2:y=ax2+bx开口大小相同、方向相反,它们相交于O,C两点,且分别与x轴的正半轴交于点B,点A,OA=2OB.
(1)求抛物线C2的解析式;
(2)在抛物线C2的对称轴上是否存在点P,使PA+PC的值最小?若存在,求出点P的坐标,若不存在,说明理由;
(3)M是直线OC上方抛物线C2上的一个动点,连接MO,MC,M运动到什么位置时,△MOC面积最大?并求出最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=4,AC与BD交于点O, N是AO的中点,点M在BC边上,且BM=3, P为对角线BD上一点,当对角线BD平分∠NPM时,PM-PN值为( )

A.1B.![]() C.2D.
C.2D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,![]() 绕某点按一定方向旋转一定角度后得到
绕某点按一定方向旋转一定角度后得到![]() ,点A,B,C分别对应点A1,B1,C1 .
,点A,B,C分别对应点A1,B1,C1 .
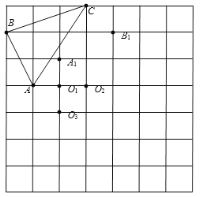
(1)根据点![]() 和
和![]() 的位置确定旋转中心是点______________.
的位置确定旋转中心是点______________.
(2)请在图中画出![]() ;
;
(3)请具体描述一下这个旋转:________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(0,2),B(2,2),C(-1,-2),抛物线F:![]() 与直线x=-2交于点P.
与直线x=-2交于点P.
(1)当抛物线F经过点C时,求它的表达式;
(2)设点P的纵坐标为![]() ,求
,求![]() 的最小值,此时抛物线F上有两点
的最小值,此时抛物线F上有两点![]() ,
,![]() ,且
,且![]() ≤-2,比较
≤-2,比较![]() 与
与![]() 的大小;
的大小;
(3)当抛物线F与线段AB有公共点时,直接写出m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C:y=x2+2x﹣3.
抛物线 | 顶点坐标 | 与x轴交点坐标 | 与y轴交点坐标 | |
抛物线C:y=x2+2x﹣3 | A(_____) | B(_____) | (1,0) | (0,﹣3) |
变换后的抛物线C1 | ______ | ______ | ______ | ______ |
(1)补全表中A,B两点的坐标,并在所给的平面直角坐标系中画出抛物线C.
(2)将抛物线C上每一点的横坐标变为原来的2倍,纵坐标变为原来的![]() ,可证明得到的曲线仍是抛物线,(记为C1),求抛物线C1对应的函数表达式.
,可证明得到的曲线仍是抛物线,(记为C1),求抛物线C1对应的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
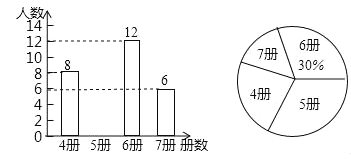
【题目】高尔基说:“书,是人类进步的阶梯.”阅读可以丰富知识、拓展视野、充实生活等诸多益处.为了解学生的课外阅读情况,某校随机抽查了部分学生阅读课外书册数的情况,并绘制出如下统计图,其中条形统计图因为破损丢失了阅读5册书数的数据.
(1)求条形图中丢失的数据,并写出阅读书册数的众数和中位数;
(2)根据随机抽查的这个结果,请估计该校1200名学生中课外阅读5册书的学生人数;
(3)若学校又补查了部分同学的课外阅读情况,得知这部分同学中课外阅读最少的是6册,将补查的情况与之前的数据合并后发现中位数并没有改变,试求最多补查了多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com