
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 与
与![]() 边交于点
边交于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
![]() 求证:
求证:![]() 是
是![]() 的切线;
的切线;
![]() 若
若![]() 的半径为
的半径为![]() ,
,![]() ,求
,求![]() 的长.
的长.

【答案】(1)见解析;(2)![]() .
.
【解析】
(1)连接OD,根据等边对等角得到∠A=∠ADO,再结合平行线的性质可得到∠DOE=∠COE,从而得到△ODE≌△OCE,根据全等三角形的性质得到∠ODE=∠ACB=90°,由此得到结论;
(2)连接CD,根据平行线等分线段定理得到BE=CE,根据勾股定理得到AB=10,由三角形的面积公式得到CD的长.在Rt△CBD中,由勾股定理即可得到结论.
(1)连接OD.
∵OA=OD,∴∠A=∠ADO.
∵OE∥AB,∴∠A=∠EOC,∠ADO=∠DOE,∴∠DOE=∠COE.
在△ODE与△OCE中,∵OD=OC,∠DOE=∠COE,OE=OE,∴△ODE≌△OCE,∴∠ODE=∠ACB=90°,∴DE是⊙O的切线;
(2)连接CD.
∵OE∥AB,AO=OC,∴BE=EC.
∵⊙O的半径为3,EC=4,∴BC=8,AC=6.
∵∠ACB=90°,∴AB=10.
∵AC是直径,∴∠ADC=90°.
∵S△ABC=![]() ACBC=
ACBC=![]() ABCD,∴6×8=10×CD,解得:CD=
ABCD,∴6×8=10×CD,解得:CD=![]() ,∴BD=
,∴BD=![]() =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图:把一张给定大小的矩形卡片ABCD放在宽度为10mm的横格纸中,恰好四个顶点都在横格线上,已知α=25°,求长方形卡片的周长。(精确到1mm,参考数据: sin25°≈0,cos25°≈0.9,tan25°≈0.5).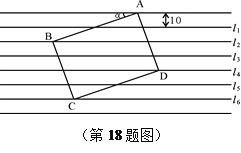
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中考英语听力测试期间T需要杜绝考点周围的噪音.如图,点A是某市一中考考点,在位于考点南偏西15°方向距离500米的C点处有一消防队.在听力考试期间,消防队突然接到报警电话,消防车需沿北偏东75°方向的公路CF前往救援.已知消防车的警报声传播半径为400米,若消防车的警报声对听力测试造成影响,则消防车必须改道行驶.试问:消防车是否需要改道行驶?
说明理由.(![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是__________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:如图1所示的图形,像我们常见的学习用品—圆规.我们不妨把这样图形叫做“规形图”.
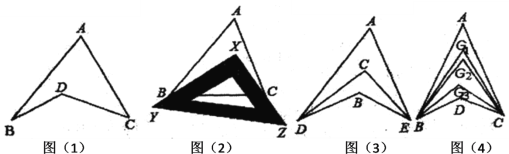
(1)观察“规形图”,试探究![]() 与
与![]() 、
、![]() 、
、![]() 之间的关系,并说明理由;
之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺![]() 放置在
放置在![]() 上,使三角尺的两条直角边
上,使三角尺的两条直角边![]() 、
、![]() 恰好经过点
恰好经过点![]() 、
、![]() ,
,![]() ,则
,则![]() ________________;
________________;
②如图3,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
③如图4,![]() ,
,![]() 的
的![]() 等分线相交于点
等分线相交于点![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
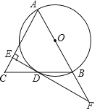
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 的弦,延长
的弦,延长![]() 到点
到点![]() ,使
,使![]() ,连结
,连结![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
![]() 求证:
求证:![]() 为
为![]() 的切线;
的切线;
![]() 猜想线段
猜想线段![]() 、
、![]() 、
、![]() 之间的数量关系,并证明你的猜想;
之间的数量关系,并证明你的猜想;
![]() 若
若![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
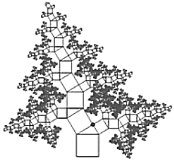
【题目】勾股定理揭示了直角三角形三边之间的关系,其中蕴含着丰富的科学知识和人文价值.如图所示,是一棵由正方形和含![]() 角的直角三角形按一定规律长成的勾股树,树的主干自下而上第一个正方形和第一个直角三角形的面积之和为
角的直角三角形按一定规律长成的勾股树,树的主干自下而上第一个正方形和第一个直角三角形的面积之和为![]() ,第二个正方形和第二个直角三角形的面积之和为
,第二个正方形和第二个直角三角形的面积之和为![]() ,…,第
,…,第![]() 个正方形和第
个正方形和第![]() 个直角三角形的面积之和为
个直角三角形的面积之和为![]() .
.
设第一个正方形的边长为1.
请解答下列问题:
(1)![]() ______.
______.
(2)通过探究,用含![]() 的代数式表示
的代数式表示![]() ,则
,则![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
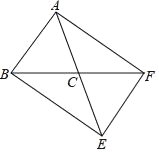
【题目】如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△EFC,连接AF、BE.
(1)求证:四边形ABEF是平行四边形;
(2)当∠ABC为多少度时,四边形ABEF为矩形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于钝角β,定义它的三角函数值如下:
sinβ=sin(180°﹣β),cosβ=﹣cos(180°﹣β),tanβ=﹣tan(180°﹣β).
(1)求sin120°,cos135°,tan150°的值;
(2)若一个三角形的三个内角的比是1:1:4,A,B是这个三角形的两个顶点,sinA,cosB是方程ax2﹣bx﹣1=0的两个不相等的实数根,求a、b的值及∠A和∠B的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com