
【题目】对于钝角β,定义它的三角函数值如下:
sinβ=sin(180°﹣β),cosβ=﹣cos(180°﹣β),tanβ=﹣tan(180°﹣β).
(1)求sin120°,cos135°,tan150°的值;
(2)若一个三角形的三个内角的比是1:1:4,A,B是这个三角形的两个顶点,sinA,cosB是方程ax2﹣bx﹣1=0的两个不相等的实数根,求a、b的值及∠A和∠B的大小.
【答案】(1)![]() ,
,![]() ,-
,-![]() (2)当A=B=30°时,a=﹣
(2)当A=B=30°时,a=﹣![]() ,b=﹣2﹣
,b=﹣2﹣![]() ;当A=30°、B=120°时,a=4,b=0
;当A=30°、B=120°时,a=4,b=0
【解析】
(1)根据给定钝角的三角函数值,代入数据,即可求出结论;
(2)根据三角形的内角和定理以及三个角的比例可得出三角形的三个内角,分①A=B=30°;②A=30°、B=120°;③A=120°、B=30°.三种情况考虑,根据特殊角的三角函数值找出sinA、cosB的值,再根据根与系数的关系找出关于a、b的二元一次方程组,解方程组即可得出结论.
(1)sin120°=sin(180°﹣120°)=sin60°=![]() ;
;
cos135°=﹣cos(180°﹣135°)=﹣cos45°=﹣![]() ;
;
tan150°=﹣tan(180°﹣150°)=﹣tan30°=﹣![]() .
.
(2)∵一个三角形的三个内角的比是1:1:4,且三角形的内角和为180°,
∴三角形的三个内角为30、30、120.
①当A=30°、B=30°时,sinA=![]() ,cosB=
,cosB=![]() ,
,
∵sinA,cosB是方程ax2﹣bx﹣1=0的两个不相等的实数根,
∴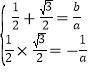 ,
,
解得:a=﹣![]() ,b=﹣2﹣
,b=﹣2﹣![]() ;
;
②当A=30°、B=120°时,sinA=![]() ,cosB=﹣
,cosB=﹣![]() ,
,
∵sinA,cosB是方程ax2﹣bx﹣1=0的两个不相等的实数根,
∴ ,
,
解得:a=4,b=0;
③当A=120°、B=30°时,sinA=![]() ,cosB=
,cosB=![]() ,
,
此时sinA=cosB,不满足题意.
综上可知:当A=B=30°时,a=﹣![]() ,b=﹣2﹣
,b=﹣2﹣![]() ;当A=30°、B=120°时,a=4,b=0.
;当A=30°、B=120°时,a=4,b=0.


科目:初中数学 来源: 题型:
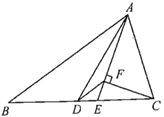
【题目】如图所示,在![]() 中,AB>AC,AD是中线,AE是角平分线,CF⊥AE于点F,连接DF,则①DF//AB;②∠DAE=
中,AB>AC,AD是中线,AE是角平分线,CF⊥AE于点F,连接DF,则①DF//AB;②∠DAE=![]() (∠ACB-∠ABC);③DF=
(∠ACB-∠ABC);③DF=![]() (AB-AC);④
(AB-AC);④![]() (AB-AC)<AD<
(AB-AC)<AD<![]() (AB+AC).其中正确的是__________.
(AB+AC).其中正确的是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),点D的坐标为(2,0),E为AB上的点,当△CDE的周长最小时,点E的坐标为( )
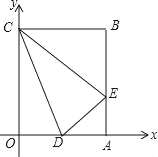
A. (1,3) B. (3,1) C. (4,1) D. (3,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位运动员在距篮下4m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离是2.5m时,达到最大高度3.5m,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05m.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式.
(2)该运动员身高1.8m,在这次跳投中,球在头顶上0.25m处出手,
问:球出手时,他距离地面的高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】被历代数学家尊为“算经之首”的《九章算术》是中国古代算法的扛鼎之作.《九章算术》中记载:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”
译文:“今有5只雀、6只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.5只雀、6只燕重量为1斤.问雀、燕毎只各重多少斤?”
设每只雀重x斤,每只燕重y斤,可列方程组为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ACB=90°,AC > BC,CD是Rt△ABC的高,E是AC的中点,ED的延长线与CB的延长线相交于点F.
(1)求证:DF是BF和CF的比例中项;
(2)在AB上取一点G,如果AE·AC=AG·AD,求证:EG·CF=ED·DF.

查看答案和解析>>
科目:初中数学 来源: 题型:
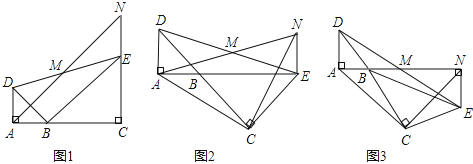
【题目】如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3位置时,(2)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com