
【题目】如图,点![]() 是
是![]() 的角平分线
的角平分线![]() 上一点,
上一点,![]() 于点
于点![]() ,点
,点![]() 是线段
是线段![]() 上一点.已知
上一点.已知![]() ,
,![]() ,点
,点![]() 为
为![]() 上一点.若满足
上一点.若满足![]() ,则
,则![]() 的长度为( )
的长度为( )
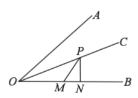
A.3B.5C.5和7D.3或7
【答案】D
【解析】
过点P作PE⊥AO于E,根据角平分线的性质和定义可得PE=PN,∠POE=∠PON,∠PEO=∠PNO=90°,再根据角平分线的性质可得OE=ON=5,然后根据点D与点E的先对位置分类讨论,分别画出对应的图形,利用HL证出Rt△PDE≌Rt△PMN,可得DE=MN,即可求出OD.
解:过点P作PE⊥AO于E
∵OC平分∠AOB,![]() ,
,
∴PE=PN,∠POE=∠PON,∠PEO=∠PNO=90°
∴∠OPE=90°-∠POE=90°-∠PON=∠OPN
∴PO平分∠EPN
∴OE=ON=5
①若点D在点E左下方时,连接PD,如下图所示
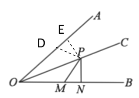
在Rt△PDE和Rt△PMN中
![]()
∴Rt△PDE≌Rt△PMN
∴DE=MN
∵MN=ON-OM=2
∴DE=2
∴OD=OE-DE=3
②若点D在点E右上方时,连接PD,如下图所示
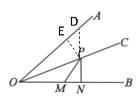
在Rt△PDE和Rt△PMN中
![]()
∴Rt△PDE≌Rt△PMN
∴DE=MN
∵MN=ON-OM=2
∴DE=2
∴OD=OE+DE=7
综上所述:OD=3或7.
故选D.


科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 的弦,延长
的弦,延长![]() 到点
到点![]() ,使
,使![]() ,连结
,连结![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
![]() 求证:
求证:![]() 为
为![]() 的切线;
的切线;
![]() 猜想线段
猜想线段![]() 、
、![]() 、
、![]() 之间的数量关系,并证明你的猜想;
之间的数量关系,并证明你的猜想;
![]() 若
若![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
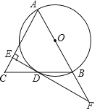
查看答案和解析>>
科目:初中数学 来源: 题型:
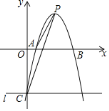
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,其顶点为
,其顶点为![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() .
.
(1)求点![]() ,
,![]() 的坐标;
的坐标;
(2)直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 的面积等于
的面积等于![]() 的面积的
的面积的![]() 倍?若存在,求出点
倍?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC平分钝角∠BAE交过B点的直线于点C,BD平分∠ABC交AC于点D,且∠BAD+∠ABD=90°.
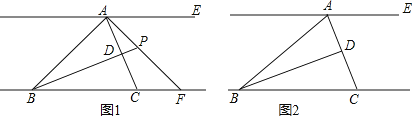
(1)求证:AE∥BC;
(2)点F是射线BC上一动点(点F不与点B,C重合),连接AF,与射线BD相交于点P.
(ⅰ)如图1,若∠ABC=45°,AF⊥AB,试探究线段BF与CF之间满足的数量关系;
(ⅱ)如图2,若AB=10,S△ABC=30,∠CAF=∠ABD,求线段BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于钝角β,定义它的三角函数值如下:
sinβ=sin(180°﹣β),cosβ=﹣cos(180°﹣β),tanβ=﹣tan(180°﹣β).
(1)求sin120°,cos135°,tan150°的值;
(2)若一个三角形的三个内角的比是1:1:4,A,B是这个三角形的两个顶点,sinA,cosB是方程ax2﹣bx﹣1=0的两个不相等的实数根,求a、b的值及∠A和∠B的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
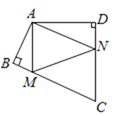
【题目】如图,在四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使三角形AMN周长最小时,则∠MAN的度数为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同.
(1)若他去买一瓶饮料,则他买到奶汁的概率是 ;
(2)若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶汁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
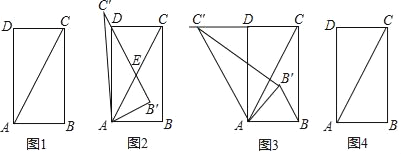
在综合与实践课上,老师组织同学们以“直角三角形的旋转”为主题开展数学活动.如图1,矩形ABCD中,AD=2AB,连接AC,将△ABC绕点A旋转到某一位置,观察图形,提出问题并加以解决.
实践操作
(1)如图2,慎思组的同学将图1中的△ABC以点A为旋转中心,按逆时针方向旋转,得到△A'B'C',此时B'C过点D,则∠ADB= 度.
(2)博学组的同学在图2的基础上继续旋转到图3,此时点C'落在CD的延长线上,连接BB',该组提出下面两个问题:
①C'D和AB有何数量关系?并说明理由.
②BB'和AC′有何位置关系?并说明理由.
请你解决该组提出的这两个问题.
提出问题
(3)请你参照以上操作,将图1中的△ABC旋转至某一位置,在图4中画出新图形,表明字母,说明构图方法,并提出一个问题,不必解答.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com