
【题目】综合与实践
问题情境
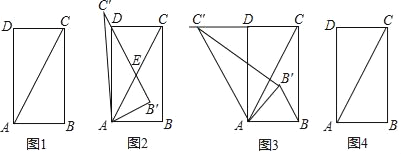
在综合与实践课上,老师组织同学们以“直角三角形的旋转”为主题开展数学活动.如图1,矩形ABCD中,AD=2AB,连接AC,将△ABC绕点A旋转到某一位置,观察图形,提出问题并加以解决.
实践操作
(1)如图2,慎思组的同学将图1中的△ABC以点A为旋转中心,按逆时针方向旋转,得到△A'B'C',此时B'C过点D,则∠ADB= 度.
(2)博学组的同学在图2的基础上继续旋转到图3,此时点C'落在CD的延长线上,连接BB',该组提出下面两个问题:
①C'D和AB有何数量关系?并说明理由.
②BB'和AC′有何位置关系?并说明理由.
请你解决该组提出的这两个问题.
提出问题
(3)请你参照以上操作,将图1中的△ABC旋转至某一位置,在图4中画出新图形,表明字母,说明构图方法,并提出一个问题,不必解答.
【答案】(1)30(2)①C′D=AB②见解析(3)见解析
【解析】
(1)由旋转性质知AB=AB′、∠B′=∠B=90°,结合AD=BC=2AB可得AD=2AB′,根据直角三角形的性质即可求解;(2)①C′D=AB,利用“HL”证Rt△ADC′≌Rt△ABC即可得;②过点C′作C′H垂直于BA延长线于点H,证△C′HA≌△C′B′A得∠HAC′=∠C′AB,由AB=AB′知∠ABB′=∠AB′B,据此根据∠HAB′=∠ABB′+∠AB′B可得2∠C′AB′=2∠AB′B,即可证得结论;(3)将△ABC以点A为旋转中心,按逆时针方向旋转得△AB′C′,AB′与对角线AC重合时,B′C′与AD交于点M,求S△AB′M:S△ADC的值?利用相似三角形的判定与性质即可解决此题.
(1)由题意知△ABC≌△AB′C′,
∴AB=AB′、∠B′=∠B=90°,
∵AD=BC=2AB,
∴在Rt△AB′D中,AD=2AB′,
则∠ADB′=30°,
故答案为:30;
(2)①C′D=AB,理由如下:
∵四边形ABCD是矩形,
∴AD=BC、∠ABC=∠ADC=∠ADC′=90°,
由旋转知AC′=AC,
在Rt△ADC′和Rt△ABC中,
∵![]() ,
,
∴Rt△ADC′≌Rt△ABC(HL),
∴C′D=AB;
②如图a,过点C′作C′H垂直于BA延长线于点H,

则四边形HADC′是矩形,
∴C′H=AD、AH=C′D=AB,
在△C′HA和△C′B′A中,
∵ ,
,
∴△C′HA≌△C′B′A(SSS),
∴∠HAC′=∠C′AB,
又∵AB=AB′,
∴∠ABB′=∠AB′B,
在△ABB′中,∠HAB′=∠ABB′+∠AB′B,即∠HAC′+∠C′AB′=∠ABB′+∠AB′B,
∴2∠C′AB′=2∠AB′B,
∴∠C′AB′=∠AB′B,
∴AC′∥BB′;
(3)如图b,
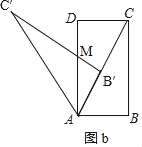
将△ABC以点A为旋转中心,按逆时针方向旋转得△AB′C′,AB′与对角线AC重合时,B′C′与AD交于点M,求S△AB′M:S△ADC的值?


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+mx+n与直线y=﹣
x2+mx+n与直线y=﹣![]() x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
(1)求抛物线的关系式和tan∠BAC的值;
(2)P为抛物线上一动点,连接PA,过点P作PQ⊥OA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ACB相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由;
(3)在AB上找一点M,使得OM+DM的值最小,直接写出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2![]() cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
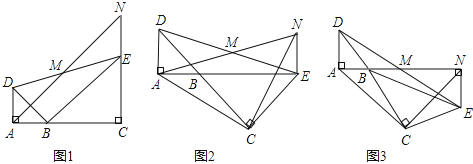
【题目】如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3位置时,(2)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图反映是小明从家去食堂吃早餐,接着去图书馆读报,然后回家的过程.其中x表示时间,y表示小明离家的距离,小明家、食堂、图书馆在同一直线上.根据图中提供的信息,解答下列问题:
(1)食堂离小明家___________km;
(2)小明在食堂吃早餐用了 分钟,在图书馆读报用了______min;
(3)由图象知:_________位于________和__________之间( 填“小明家”、“食堂”、“图书馆” )
(4)求小明从图书馆回家的平均速度是多少千米/时?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是⊙O的直径,AB=10, ![]() ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=
,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=![]() ∠AOD;③DM⊥CE;④CM+DM的最小值是10,其中正确的序号是______.
∠AOD;③DM⊥CE;④CM+DM的最小值是10,其中正确的序号是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人加工同一种零件,甲每天加工的数量是乙每天加工数量的1.5倍,两人各加工600个这种零件,甲比乙少用5天.
(1)甲、乙两人每天各加工多少个这种零件?
(2)已知甲、乙两人加工这种零件每天的加工费分别是150元和120,现有1600个这种零件的加工任务,甲单独加工一段时间后另有安排,剩余任务由乙单独完成.如果总加工费不超过4200元,那么甲至少加工了多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com