
【题目】出租车司机小傅某天下午营运全是在东西走向的大道上行驶的.若如果规定向东为正,则行车里程(单位:km)如下:
+11,-2,+3,+10,-11,+5,-15,-8
(1)当把最后一名乘客送到目的地时,小傅距离出车地点的距离为多少?
(2)若每千米的营运额为7元,成本为1.5元/km,则这天下午他盈利多少元?
科目:初中数学 来源: 题型:
【题目】某出租车司机从公司出发,在东西方向的人民路上连续接送![]() 批客人,行驶路程记录如下(规定向东为正,向西为负,单位:
批客人,行驶路程记录如下(规定向东为正,向西为负,单位:![]() ):
):
第 | 第 | 第 | 第 | 第 |
|
|
|
|
|
(1)接送完第![]() 批客人后,该驾驶员在公司什么方向,距离公司多少千米?
批客人后,该驾驶员在公司什么方向,距离公司多少千米?
(2)若该出租车每千米耗油![]() 升,那么在这过程中共耗油多少升?
升,那么在这过程中共耗油多少升?
(3)若该出租车的计价标准为:行驶路程不超过![]() 收费
收费![]() 元,超过
元,超过![]() 的部分按每千米
的部分按每千米![]() 元收费,在这过程中该驾驶员共收到车费多少元?
元收费,在这过程中该驾驶员共收到车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知(x3+mx+n)(x2﹣3x+4)展开式中不含 x3和 x2项.
(1)求m、n的值;
(2)当 m、n取第(1)小题的值时,求(m+n)(m2﹣mn+n2)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图1所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.
(1)填空:∠BAN=_____°;
(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图2,若两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作∠ACD交PQ于点D,且∠ACD=120°,则在转动过程中,请探究∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
已知:如图1,等边△A1A2A3内接于⊙O,点P是![]() 上的任意一点,连接PA1,PA2,PA3,可证:PA1+PA2=PA3,从而得到:
上的任意一点,连接PA1,PA2,PA3,可证:PA1+PA2=PA3,从而得到:![]() 是定值.
是定值.
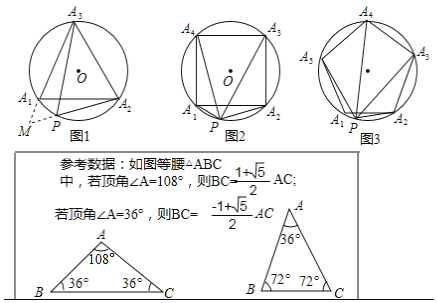
(1)以下是小红的一种证明方法,请在方框内将证明过程补充完整;
证明:如图1,作∠PA1M=60°,A1M交A2P的延长线于点M.
∵△A1A2A3是等边三角形,
∴∠A3A1A2=60°,
∴∠A3A1P=∠A2A1M
又A3A1=A2A1,∠A1A3P=∠A1A2P,
∴△A1A3P≌△A1A2M

∴PA3=MA2=PA2+PM=PA2+PA1.
∴![]() ,是定值.
,是定值.
(2)延伸:如图2,把(1)中条件“等边△A1A2A3”改为“正方形A1A2A3A4”,其余条件不变,请问:![]() 还是定值吗?为什么?
还是定值吗?为什么?
(3)拓展:如图3,把(1)中条件“等边△A1A2A3”改为“正五边形A1A2A3A4A5”,其余条件不变,则![]() = (只写出结果).
= (只写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.
(1)农民自带的零钱是多少?
(2)试求降价前y与x之间的关系式
(3)由表达式你能求出降价前每千克的土豆价格是多少?
(4)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
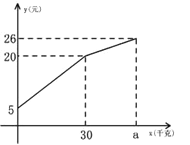
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系![]() 中,已知点
中,已知点![]() 和点
和点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 按顺时针分别旋转
按顺时针分别旋转![]() ,
,![]() 得到
得到![]() ,
,![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,
,![]() ,
,![]() ;抛物线
;抛物线![]() 经过点
经过点![]() ,
,![]() ,
,![]() .
.

(1)点![]() 的坐标为________,点
的坐标为________,点![]() 的坐标为________;抛物线
的坐标为________;抛物线![]() 的解析式为________,抛物线
的解析式为________,抛物线![]() 的解析式为________;
的解析式为________;
(2)如果点![]() 是直线
是直线![]() 上方抛物线
上方抛物线![]() 上的一个动点.
上的一个动点.
①若![]() ,求
,求![]() 点的坐标;
点的坐标;
②如图2,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,交抛物线
,交抛物线![]() 于点
于点![]() ,记
,记![]() ,求
,求![]() 与
与![]() 的函数关系式.当
的函数关系式.当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com