
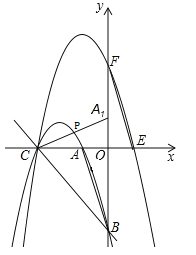
【题目】如图1,在平面直角坐标系![]() 中,已知点
中,已知点![]() 和点
和点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 按顺时针分别旋转
按顺时针分别旋转![]() ,
,![]() 得到
得到![]() ,
,![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,
,![]() ,
,![]() ;抛物线
;抛物线![]() 经过点
经过点![]() ,
,![]() ,
,![]() .
.

(1)点![]() 的坐标为________,点
的坐标为________,点![]() 的坐标为________;抛物线
的坐标为________;抛物线![]() 的解析式为________,抛物线
的解析式为________,抛物线![]() 的解析式为________;
的解析式为________;
(2)如果点![]() 是直线
是直线![]() 上方抛物线
上方抛物线![]() 上的一个动点.
上的一个动点.
①若![]() ,求
,求![]() 点的坐标;
点的坐标;
②如图2,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,交抛物线
,交抛物线![]() 于点
于点![]() ,记
,记![]() ,求
,求![]() 与
与![]() 的函数关系式.当
的函数关系式.当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ,
,![]() :
:![]() ,
,![]() :
:![]() .(2)①符合条件的点
.(2)①符合条件的点![]() 的坐标为
的坐标为![]() 或
或![]() .②
.②![]() .
.
【解析】
(1)根据旋转的性质,可得C,E,F的坐标,根据待定系数法求解析式;
(2)①根据P点关于直线CA或关于x轴对称直线与抛物线交点坐标,求出解析式,联立方程组求解;
②根据图象上的点满足函数解析式,可得P、N、M纵坐标,根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得二次函数,根据x取值范围讨论h范围.
(1)由旋转可知,OC=6,OE=2,
则点C坐标为(-6,0),E点坐标为(2,0),
分别利用待定系数法求C1解析式为:y=-![]() x24x6,C2解析式为:y=-
x24x6,C2解析式为:y=-![]() x22x+6
x22x+6
(2)①若点P在x轴上方,∠PCA=∠ABO时,则CA1与抛物线C1的交点即为点P,如图,
设直线CA1的解析式为:y=k1x+b1
∴![]()
解得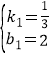
∴直线CA1的解析式为:y=![]() x+2
x+2
联立: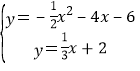 ,解得
,解得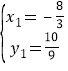 或
或![]() (舍去),
(舍去),
∴P(![]() )
)
若点P在x轴下方,∠PCA=∠ABO时,则CH与抛物线C1的交点即为点P,如图,
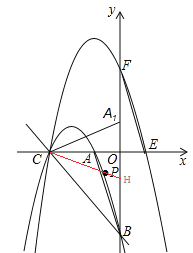
易知OH=OA,
∴H(0,-2)
设直线CH的解析式为:y=k2x+b2
∴![]()
解得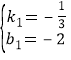
∴直线CH的解析式为:y=![]() x-2
x-2
联立: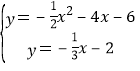 ,解得
,解得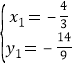 或
或![]() (舍去),
(舍去),
∴![]() ;
;
∴符合条件的点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
②设直线![]() 的解析式为:
的解析式为:![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴直线![]() 的解析式为:
的解析式为:![]() ,
,
过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() ,
,

设P(x,-![]() x24x6)
x24x6)
∴![]() ,
,
![]()
![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,
时,![]() 的最大值为21.
的最大值为21.
∵![]() ,当
,当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】出租车司机小傅某天下午营运全是在东西走向的大道上行驶的.若如果规定向东为正,则行车里程(单位:km)如下:
+11,-2,+3,+10,-11,+5,-15,-8
(1)当把最后一名乘客送到目的地时,小傅距离出车地点的距离为多少?
(2)若每千米的营运额为7元,成本为1.5元/km,则这天下午他盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车销售公司经销某品牌A款汽车,随着汽车的普及,其价格也在不断下降,今年5月份A款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的A款汽车,去年销售额为90万元,今年销售额只有80万元.
(1)今年5月份A款汽车每辆售价多少万元?
(2)为了增加收入,汽车销售公司决定再经销同品牌的B款汽车,已知B款汽车每辆进价为7.5万元,每辆售价为10.5万元,A款汽车每辆进价为6万元,若卖出这两款汽车15辆后获利不低于38万元,问B款汽车至少卖出多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2开始的连续偶数相加,它们和的情况如下表:
加数的个数(n) | 和(S) |
1 | 2=1×2 |
2 | 2+4=6=2×3 |
3 | 2+4+6=12=3×4 |
4 | 2+4+6+8=20=4×5 |
5 | 2+4+6+8+10=30=5×6 |
… | … |
(1)根据表中的规律,直接写出2+4+6+8+10+12+14=________
(2)根据表中的规律猜想:S=2+4+6+8+…+2n=___________(用n的代数式表示);
(3)利用上题中的公式计算102+104+106+…+200的值(要求写出计算过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC与△CDE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④∠BOC=∠EOC.其中正确结论的个数为

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(4,0),B(0,3),C(4,3),I是△ABC的内心,将△ABC绕原点逆时针旋转90°后,I的对应点I'的坐标为( )
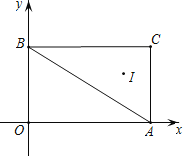
A. (﹣2,3) B. (﹣3,2) C. (3,﹣2) D. (2,﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
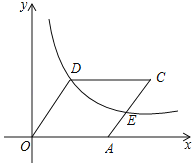
【题目】如图,在平面直角坐标系xOy中,函数y=![]() (k>0,x>0)的图象经过菱形OACD的顶点D和边AC的中点E,若菱形OACD的边长为3,则k的值为_____.
(k>0,x>0)的图象经过菱形OACD的顶点D和边AC的中点E,若菱形OACD的边长为3,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,老师出示了如下的题目:“在等边△ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图1,试确定线段AE与DB的大小关系,并说明理由.”小敏与同桌小聪讨论后,进行了如下解答:
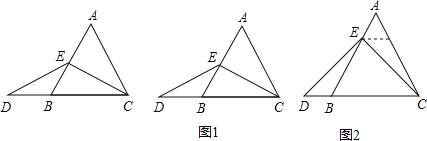
(1)特殊情况,探索结论:当点E为AB的中点时,如图1,确定线段AE与DB的大小关系,请你直接写出结论:AE DB(填“≥”,“≤”或“=”)
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“≥”,“≤”或“=”).理由如下:如图3,过点E做EF∥BC,交AC于点F.(请你完成解答过程)
(3)拓展结论,设计新题.
已知O是等边三角形ABD的边BD的中点,AB=4,EF分别为射线AB、DA上一动点,且∠EOF=120°,若AF=1,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校要从小红、小明和小亮三名同学中挑选一名同学参加数学素养大赛,在最近的四次专题测试中,他们三人的成绩如下表所示:
学生 专题 | 集合证明 | PISA问题 | 应用题 | 动点问题 |
小红 | 70 | 75 | 80 | 85 |
小明 | 80 | 80 | 72 | 76 |
小亮 | 75 | 75 | 90 | 65 |
(1)请算出小红的平均分为多少?
(2)该校根据四次专题考试成绩的重要程度不同而赋予每个专题成绩一个权重,权重比依次为x:1:2:1,最后得出三人的成绩(加权平均数),若从高分到低分排序为小亮、小明、小红,求正整数x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com