
【题目】如图①,在正方形![]() 中,
中,![]() ,
,![]() 为对角线
为对角线![]() 上任意一点(不与
上任意一点(不与![]() 重合),连接
重合),连接![]() ,过点
,过点![]() 作
作![]() ,交线段
,交线段![]() 于点
于点![]() .
.
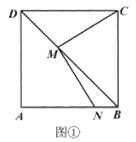
(1)求证:![]() ;
;
(2)若![]() ,求证:
,求证:![]() ;
;
(3)如图②,连接![]() 交
交![]() 于点
于点![]() .若
.若![]() ,求
,求![]() 的值.
的值.
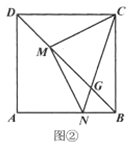
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
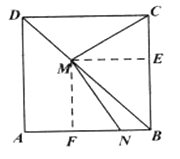
(1)如图,过![]() 分别作
分别作![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,则四边形
,则四边形![]() 是平行四边形,先证明四边形
是平行四边形,先证明四边形![]() 是正方形,继而证明
是正方形,继而证明![]() ,即可得结论;
,即可得结论;
(2)由(1)得![]() ,
,![]() ,根据比例线段可得
,根据比例线段可得![]() ,
,![]() ,再根据
,再根据![]() 可得
可得![]() ,从而求得AN、BN长即可得结论;
,从而求得AN、BN长即可得结论;
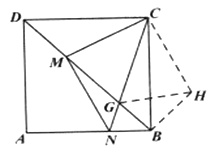
(3)把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,
,![]() ,进而可推导得出
,进而可推导得出![]() ,
,![]() ,证明
,证明![]() 是等腰直角三角形,继而证明
是等腰直角三角形,继而证明![]() ,可得MG=HG,根据题意设
,可得MG=HG,根据题意设![]() ,则
,则![]() ,根据勾股定理可求得
,根据勾股定理可求得![]() ,再结合正方形的性质可求得a的值,继而证明
,再结合正方形的性质可求得a的值,继而证明![]() , 根据相似三角形的性质即可求得答案.
, 根据相似三角形的性质即可求得答案.
(1)如图,过![]() 分别作
分别作![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,则四边形
,则四边形![]() 是平行四边形,
是平行四边形,
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() ,
,![]() ,
,
![]() ,
,
![]() 平行四边形
平行四边形![]() 是正方形,
是正方形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)由(1)得:![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ;
;
(3)把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 设
设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,则
,则![]() ,
,
![]() 正方形
正方形![]() 的边长为
的边长为![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】已知正方形MNOK和正六边形ABCDEF边长均为2,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M之间距离的最小值是_____.
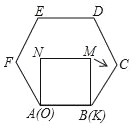
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 已知抛物线y=![]() x2+bx+c经过点A(-2,0),B(0,-4)与x轴交于另一点C,连接BC.
x2+bx+c经过点A(-2,0),B(0,-4)与x轴交于另一点C,连接BC.

(1)求抛物线的解析式;
(2)如图,P是第一象限内抛物线上一点,BP交x轴于点E,且S△PBO=S△PBC,求证:E是OC的中点;
(3)在(2)的条件下求点P的坐标.
(4)在(2)的条件下拋物线上是否存在点D,使△ACD的面积与△ABP的面积相等?若存在,请求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.

(1)求证:△BAE≌△BCF;
(2)若∠ABC=50°,则当∠EBA= °时,四边形BFDE是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)(2017·黄冈)已知:如图,一次函数y=-2x+1与反比例函数y=![]() 的图象有两个交点A(-1,m)和B,过点A作AE⊥x轴,垂足为E;过点B作BD⊥y轴,垂足为点D,且点D的坐标为(0,-2),连结DE.
的图象有两个交点A(-1,m)和B,过点A作AE⊥x轴,垂足为E;过点B作BD⊥y轴,垂足为点D,且点D的坐标为(0,-2),连结DE.
(1)求k的值;
(2)求四边形AEDB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=ax经过点A(4,2),点B在双曲线y=![]() (x>0)的图象上,连结OB、AB,若∠ABO=90°,BA=BO,则k的值为_____.
(x>0)的图象上,连结OB、AB,若∠ABO=90°,BA=BO,则k的值为_____.
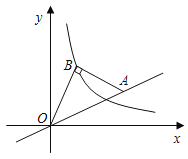
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师留在小黑板上的题如图所示.小彬说:该抛物线过点![]() ;小明说:
;小明说:![]() ;小颖说:该抛物线在
;小颖说:该抛物线在![]() 轴上截得的线段长为
轴上截得的线段长为![]() .你认为三人的说法中,正确的有( )
.你认为三人的说法中,正确的有( )

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com