
【题目】如图,在等边![]() 和等边
和等边![]() 中,过
中,过![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() .
.
(1)如图,求证:四边形![]() 为菱形;
为菱形;
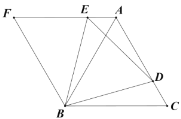
(2)如图,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,不添加任何辅助线,直接写出与
,不添加任何辅助线,直接写出与![]() 相等的所有角(不包括
相等的所有角(不包括![]() ).
).
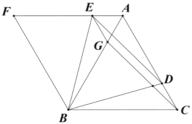
【答案】(1)见详解;(2)与![]() 相等的角有∠ABE,∠CBD,∠ACG,∠DEG.
相等的角有∠ABE,∠CBD,∠ACG,∠DEG.
【解析】
(1)由等边三角形的性质,得到AB=BC=AC,BE=BD,∠ABC=∠BAC=∠EBD=60°,先证明△ABE≌△CBD,则∠BEF=∠BDA,然后证明△FEB≌△ADB,则BF=BA=AC,则四边形AFBC是平行四边形,由BC=AC,即可得到答案;
(2)由三角形的内角和定理,得到∠ABE=∠ADE,由等量代换,得到∠CBD=∠ABE=∠ADE,由平行线的性质得∠ACG=∠ADE,由ASA证明△ABE≌△ACG,则CG=BE=DE,得到四边形CDEG是平行四边形,则∠DEG=∠ACG=∠ADE,即可得到答案.
解:(1)如图:
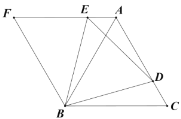
在等边![]() 和等边
和等边![]() 中,
中,
∴AB=BC=AC,BE=BD,∠ABC=∠BAC=∠EBD=60°,
∴∠ABE+∠ABD=∠ABD+∠CBD=60°,
∴∠ABE=∠CBD,
∴△ABE≌△CBD(SAS),
∴∠AEB=∠CDB,
∴∠BEF=∠BDA,
∵BF∥AC,
∴∠ABF=∠BAC=60°,
∵∠FBE+∠ABE=∠ABE+ABD=60°,
∴∠FBE=∠ABD,
∵BE=BD,
∴△FEB≌△ADB,
∴BF=BA=AC,
∴四边形AFBC是平行四边形,
∵BC=AC,
∴四边形AFBC是菱形;
(2)如图:
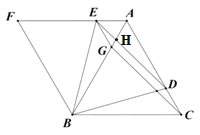
∵∠BED=∠BAC=60°,∠BHE=∠DHA,
∴∠ABE=∠ADE;
由(1)知,∠CBD=∠ABE,
∴∠CBD=∠ADE;
∵CG∥DE,
∴∠ACG=∠ADE;
∴∠ACG=∠ABE,
∵AF∥BC,
∴∠BAE=∠ABC=∠BAC=60°,
∵AB=AC,
∴△ABE≌△ACG,
∴CG=BE=DE,
∵CG∥DE,
∴四边形CDEG是平行四边形,
∴∠DEG=∠ACG=∠ADE;
∴与![]() 相等的角有:∠ABE,∠CBD,∠ACG,∠DEG.
相等的角有:∠ABE,∠CBD,∠ACG,∠DEG.


科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在边
分别在边![]() 和
和![]() 上,沿
上,沿![]() 折叠四边形
折叠四边形![]() ,使点
,使点![]() 、
、![]() 分别落在
分别落在![]() 、
、![]() 处,得四边形
处,得四边形![]() ,点
,点![]() 在
在![]() 上,过点
上,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;
;
③![]() ;④若点
;④若点![]() 是
是![]() 的中点,则
的中点,则![]() ,其中,正确结论的序号是_______.(把所有正确结论的序号都在填在横线上)
,其中,正确结论的序号是_______.(把所有正确结论的序号都在填在横线上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过![]() 和
和![]() 两点的抛物线
两点的抛物线![]() 交
交![]() 轴于
轴于![]() 两点,
两点,![]() 是抛物线上一动点,平行于
是抛物线上一动点,平行于![]() 轴的直线
轴的直线![]() 经过点
经过点![]() .
.
(1)求抛物线的解析式;
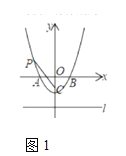
(2)如图1,![]() 轴上有点
轴上有点![]() 连接
连接![]() ,设点
,设点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.![]() .小明在探究
.小明在探究![]() 的值的过程中,是这样思考的:当
的值的过程中,是这样思考的:当![]() 是抛物线的顶点时,计算
是抛物线的顶点时,计算![]() 的值;当
的值;当![]() 不是抛物线的顶点时,猜想
不是抛物线的顶点时,猜想![]() 是一个定值.请你直接写出
是一个定值.请你直接写出![]() 的值,并证明小明的猜想.
的值,并证明小明的猜想.
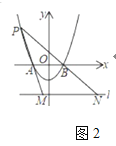
(3)如图2,点![]() 在第二象限,分别连接
在第二象限,分别连接![]() 、
、![]() ,并延长交直线
,并延长交直线![]() 于
于![]() 两点.若
两点.若![]() 两点的横坐标分别为
两点的横坐标分别为![]() ,试探究
,试探究![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边上的中线,点
边上的中线,点![]() 为线段
为线段![]() 上一点(不与点
上一点(不与点![]() 、点
、点![]() 重合),连接
重合),连接![]() ,作
,作![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,与
,与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
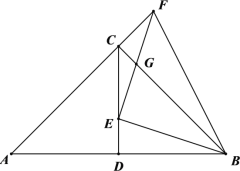
(1)求证:![]() ;
;
(2)求![]() 的度数;
的度数;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,已知抛物线![]() (a<0)与x轴交于A、B两点(点A在点B左侧),与y轴负半轴交于点C,顶点为D,已知
(a<0)与x轴交于A、B两点(点A在点B左侧),与y轴负半轴交于点C,顶点为D,已知![]() :S四边形ACBD=1:4.
:S四边形ACBD=1:4.
(1)求点D的坐标(用仅含c的代数式表示);
(2)若tan∠ACB=![]() ,求抛物线的解析式.
,求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
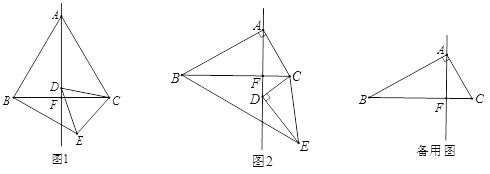
【题目】(1)问题发现:如图1,在△ABC中和△DCE中,![]() ,
,![]() ,
,![]() ,点D是BC的垂线AF上任意一点.填空:
,点D是BC的垂线AF上任意一点.填空:
①![]() 的值为 ;
的值为 ;
②∠ABE的度数为 .
(2)类比探究:如图2,在△ABC中和△DCE中,![]() ,
,![]() ,点D是BC的垂线AF上任意一点.请判断
,点D是BC的垂线AF上任意一点.请判断![]() 的值及∠ABE的度数,并说明理由;
的值及∠ABE的度数,并说明理由;
(3) 拓展延伸:在(2)的条件下,若![]() ,
,![]() ,请直接写出BE的长.
,请直接写出BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了应对全球新冠肺炎,满足抗疫物资的需求,某电机公司转型生产![]() 呼吸机和
呼吸机和![]() 呼吸机,每台
呼吸机,每台![]() 呼吸机比每台
呼吸机比每台![]() 呼吸机的生产成本多200元,用5万元生产
呼吸机的生产成本多200元,用5万元生产![]() 呼吸机与用4.5万元生产
呼吸机与用4.5万元生产![]() 呼吸机的数量相等
呼吸机的数量相等
(1)求每台![]() 呼吸机、
呼吸机、![]() 呼吸机的生产成本各是多少元?
呼吸机的生产成本各是多少元?
(2)该公司计划生产这两种呼吸机共50台进行试销,其中![]() 呼吸机为
呼吸机为![]() 台,生产总费用不超过9.8万元,试销时
台,生产总费用不超过9.8万元,试销时![]() 呼吸机每台售价2500元,
呼吸机每台售价2500元,![]() 呼吸机每台售价2180元,公司决定从销售
呼吸机每台售价2180元,公司决定从销售![]() 呼吸机的利润中按每台捐献
呼吸机的利润中按每台捐献![]() 元作为公司捐献国家抗疫的资金,若公司售完50台呼吸机并捐献资金后获得的利润不超过23000元,求
元作为公司捐献国家抗疫的资金,若公司售完50台呼吸机并捐献资金后获得的利润不超过23000元,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com