
分析 把-|-3|先化简,利用整数、负有理数、正有理数、负分数的意义,直接选择填入相对应的括号内即可.
解答 解:-|-3|=-3,--0.3=0.3
整 数{-2,-|-3|,0,5};
负 分 数{-$\frac{1}{3}$};
正有理数{$\frac{22}{7}$,--0.3,1.7,5};
负有理数{-2,-$\frac{1}{3}$,-|-3|}.
故答案为:-2,-|-3|,0,5;-$\frac{1}{3}$;$\frac{22}{7}$,--0.3,1.7,5;-2,-$\frac{1}{3}$,-|-3|.
点评 此题考查了整数、负有理数、正有理数、负分数的意义,绝对值的化简,是基础知识,需熟练掌握.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
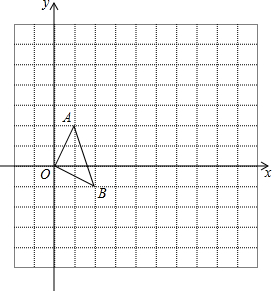 如图,在12×12的正方形网格中,△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).
如图,在12×12的正方形网格中,△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com