练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．棱长为1的正方体组成如图所示的几何体，画出该几何体的主视图和左视图．

    分析 由已知条件可知，主视图有3列，每列小正方数形数目分别为1，3，2；左视图有2列，每列小正方形数目分别为3，1．据此可画出图形．

    解答 解：如图所示：

    点评 此题考查了作图-三视图，关键明确主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形，属于基础题，难度一般．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    13．如果$\sqrt{13}$的小数部分是a，$\frac{1}{a}$的小数部分是b，则b的值是$\frac{\sqrt{13}-1}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．（1）解方程：x2=17；
    （2）将你解出的x在数轴中作出．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

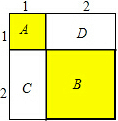    3．我们初中数学里的一些代数公式，很多都可以通过表示几何图形面积的方法进行直观推导和解释．例如：平方差公式、完全平方公式．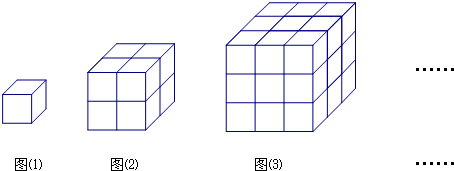
    【提出问题】如何用表示几何图形面积的方法推证：13+23=32？
    【解决问题】
    A表示1个1×1的正方形，即：1×1×1=13
    B表示1个2×2的正方形，C与D恰好可以拼成1个2×2的正方形，
    因此：B、C、D就可以表示2个2×2的正方形，即：2×2×2=23
    而A、B、C、D恰好可以拼成一个（1+2）×（1+2）的大正方形．
    由此可得：13+23=32
    【递进探究】请仿用上面的表示几何图形面积的方法探究：13+23+33=62．
    要求：自己构造图形并写出详细的解题过程．
    【推广探究】请用上面的表示几何图形面积的方法探究：13+23+33+…+n3=$\frac{{n}^{2}（n+1）^{2}}{4}$．
    （参考公式：$1+2+3+…+n=\frac{（1+n）n}{2}$）
    注意：只需填空并画出图形即可，不必写出解题过程．
    【提炼运用】如图，下列几何体是由棱长为1的小立方体按一定规律在地面上摆成的，
    如图（1）中，共有1个小立方体，其中1个看的见，0个看不见；
    如图（2）中，共有8个小立方体，其中7个看的见，1个看不见；
    如图（3）中，共有27个小立方体，其中19个看的见，8个看不见；
    求：从第（1）个图到第（101）个图中，一切看不见的棱长为1的小立方体的总个数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．我县城市居民用电收费方式有以下两种：
    类别普通电价峰谷分时电价
    时间每度0.52元峰时（8；00-21：00）谷时（21：00-8：00）
    电价每度0.55元每度0.30元
    估计小明家下月总用电量为200度，
    （1）若其中峰时电量为50度，则小明家按照哪种方式付电费比较合适？能省多少元？
    （2）请你帮小明计算，峰时电量为多少度时，两种方式所付的电费相等？
    （3）到下月付费时，小明发现那月总用电量为200度，用峰谷电价付费方式比普通电价付费方式省了14元，求那月的峰时电量为多少度？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．已知y与x-3成正比例函数，且当x=2时，y=-3．
    （1）求y与x之间的函数关系式；
    （2）求当x=1时，y的值；
    （3）求当y=-6时，x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．（1）4（2x+3）=8（1-x）-5（x-2）；
    （2）$1-\frac{7+3x}{8}=\frac{3x-10}{4}-x$；
    （3）$\frac{2-x}{2}-3=\frac{x}{3}-\frac{2x+3}{6}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．把下列各数填在相应的表示集合的大括号内-2，-$\frac{1}{3}$，-|-3|，$\frac{22}{7}$，--0.3，1.7，0，5．
    整    数{-2，-|-3|，0，5…}；
    负 分 数{-$\frac{1}{3}$…}；
    正有理数{$\frac{22}{7}$，--0.3，1.7，5…}；
    负有理数{-2，-$\frac{1}{3}$，-|-3|…}．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

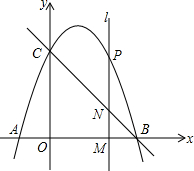    5．如图，直线BC交x轴、y轴于点B（3，0）和C（0，3），且抛物线y=-x2+bx+c过B、C两点，与x轴交于另一点A．
    （1）求直线BC和抛物线的解析式；
    （2）设P（x，y）是（1）中抛物线上的一个动点，过点P作直线l⊥x轴于点M，交直线BC于点N．
    ①若点P在第一象限内，线段PN的长度为h，试求h与x的函数解析式．h是否存在最大值？若存在，求出其最大值；若不存在，请说明理由；
    ②当△PBC是以BC为底边的等腰三角形时，则点P的坐标为（$\frac{1+\sqrt{13}}{2}$，$\frac{1+\sqrt{13}}{2}$），（$\frac{1-\sqrt{13}}{2}$，$\frac{1-\sqrt{13}}{2}$）．（直接写出坐标，不要求写解答过程）

    查看答案和解析>>

    同步练习册答案