
【题目】已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH与BE相交于点G.
(1)判断AC与图中的那条线段相等,并证明你的结论;
(2)若CE的长为 ![]() ,求BG的长.
,求BG的长.
【答案】
(1)解:证明:∵CD⊥AB,
∴∠BDC=90°,
∵∠ABC=45°,
∴△BCD是等腰直角三角形.
∴BD=CD,
∵BE⊥AC于E,
∴∠BEC=90°,
∵∠BFD=∠EFC,
∴∠DBF=∠DCA,
在Rt△DFB与Rt△DAC中,
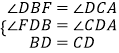 ,
,
∴Rt△DFB≌Rt△DAC,
∴BF=AC;
(2)解:∵BE平分∠ABC,

∴∠ABE=∠CBE=22.5°,
∵BE⊥AC于E,
∴∠BEA=∠BEC=90°,
又∵BE=BE,
∴Rt△BEA≌Rt△BEC,
∴CE=AE.
连结CG,
∵△BCD是等腰直角三角形,
∴BD=CD,
又H是BC边的中点,
∴DH⊥BC,
∴DH垂直平分BC,
∴BG=CG,
∵∠EBC=22.5°,
∴∠GCB=22.5°,
∴∠EGC=45°,
∴Rt△CEG是等腰直角三角形,
∵CE的长为 ![]() ,
,
∴EG= ![]() ,
,
利用勾股定理得:CE2+GE2=GC2,
∴ ![]() ,
,
∴ ![]() ,
,
∴BG的长为 ![]() .
.
【解析】(1)首先判断出△BCD是等腰直角三角形,根据等腰三角形的性质得出BD=CD,根据三角形的内角和得出∠DBF=∠DCA,然后利用AAS判断出Rt△DFB≌Rt△DAC,根据全等三角形的性质得出BF=AC;
(2)首先判断出Rt△BEA≌Rt△BEC,根据全等三角形对应边相等得出CE=AE.连结CG,根据等腰三角形的三线合一得出DH垂直平分BC,根据中垂线定理得出BG=CG,根据等边对等角得出∠EBC=22.5°=∠GCB,根据三角形的外角定理得出∠EGC=45°,故Rt△CEG是等腰直角三角形,利用勾股定理得出GC的长。
【考点精析】掌握线段垂直平分线的判定和线段垂直平分线的性质是解答本题的根本,需要知道和一条线段两个端点距离相等的点,在这条线段的垂直平分线上;垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.


科目:初中数学 来源: 题型:
【题目】如图,有一个边长不定的正方形![]() ,它的两个相对的顶点
,它的两个相对的顶点![]() 分别在边长为1的正六边形一组平行的对边上,另外两个顶点
分别在边长为1的正六边形一组平行的对边上,另外两个顶点![]() 在正六边形内部(包括边界),则正方形边长
在正六边形内部(包括边界),则正方形边长![]() 的取值范围是 .
的取值范围是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红家最近新盖了房子,室内装修时,木工师傅让小红爸爸去建材市场买一块长3m,宽2.2m的薄木板用来做家居面,到了市场爸爸看到满足这个尺寸的木板有点大,买还是不买爸爸犹豫了,因为他知道他家门框高只有2m,宽只有1m,他不知道这块木板买回家后能不能完整的通过自家门框.请你替小红爸爸解决一下难题,帮他算一算要买的木板能否通过自家门框进入室内.(备用图可供做题参考,薄木板厚度可以忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列运动:①人乘电梯,从一楼上到二楼的运动;②被投掷出去的铅球的运动;③温度计中,液面的升降运动;④在笔直的铁轨上,火车的运动.其中属于平移的有().
A.1种B.2种C.3种D.4种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC,AD,AB于点E,O,F,连接OC,OB,则图中全等的三角形有( )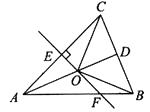
A.1对
B.2对
C.3对
D.4对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com