
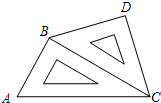
 如图所示,把一副直角三角板摆放在一起,∠ACB=30°,∠BCD=45°,∠ABC=∠BDC=90°,量得CD=20CM,试求BC、AC的长.
如图所示,把一副直角三角板摆放在一起,∠ACB=30°,∠BCD=45°,∠ABC=∠BDC=90°,量得CD=20CM,试求BC、AC的长. 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 分析探索题:细心观察如图,认真分析各式,然后解答问题.
分析探索题:细心观察如图,认真分析各式,然后解答问题.| 1 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| 3 |
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 0 | +3 -5 |
| A、100mm | B、98mm |
| C、104mm | D、96mm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com