
【题目】如图,⊙![]() 是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙
是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙![]() 于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF。
于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF。
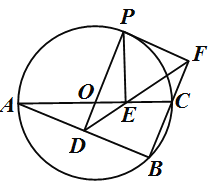
(1)、若∠POC=60°,AC=12,求劣弧PC的长;(结果保留π)
(2)、求证:OD=OE;
(3)、求证:PF是⊙![]() 的切线。
的切线。
【答案】(1)、2π;(2)、证明过程见解析;(3)、证明过程见解析.
【解析】试题分析:(1)、根据直径得出半径的长度,然后根据弧长的计算公式进行求解;(2)、根据垂直得出∠ADO=∠PEO,对顶角相等,半径相等得出△ADO和△PEO全等,从而得出OD=OE;(3)、连接PC,根据直径得出∠ABC=90°,从而说明PD∥BC,根据已知条件结合(2)得出△PCE和△PFC全等,从而说明∠OPF=90°,得出切线.
试题解析:(1)、由直径AC=12得半径OC=6 劣弧PC的长为![]()
(2)、∵ OD⊥AB,PE⊥AC ∴ ∠ADO=∠PEO=90°
在△ADO和△PEO中,∠ADO=∠PEO,∠AOD=∠POE,OA=OP ∴ △ADO≌△PEO ∴ OD=OE
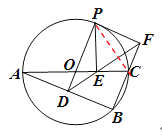
(3)、连接PC,由AC是直径知BC⊥AB,又OD⊥AB, ∴ PD∥BF
∴ ∠OPC=∠PCF,∠ODE=∠CFE 由(2)知OD=OE,则∠ODE=∠OED,又∠OED=∠FEC
∴ ∠FEC=∠CFE ∴ EC=FC 由OP=OC知∠OPC=∠OCE
∴ ∠PCE =∠PCF 在△PCE和△PFC中, EC=FC ∠PCE=∠PCF PC=PC
∴ △PCE≌△PFC ∴ ∠PFC =∠PEC=90° 由∠PDB=∠B=90°可知∠OPF=90°即OP⊥PF
∴ PF是⊙![]() 的切线
的切线


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】先阅读下列一段文字,在回答后面的问题.
已知在平面内两点P1(x1,y1)、P2(x2,y2),其两点间的距离公式![]() ,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.
,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.
(1)已知A(2,4)、B(﹣3,﹣8),试求A、B两点间的距离;
(2)已知A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A、B两点间的距离.
(3)已知一个三角形各顶点坐标为A(0,6)、B(﹣3,2)、C(3,2),你能判定此三角形的形状吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形ABCD的顶点坐标分别为 A(1,1),B(1,-1),C(-1,-1),D(-1,1),y轴上有一点 P(0,2).作点P关于点A的对称点P1,作点P1关于点B的对称点P2,作点P2关于点C的对称轴P3,作点P3关于点D的对称点P4,作点P4关于点A的对称点P5,作点P5关于点B的对称点P6,…,按此操作下去,则点P2016的坐标为( )
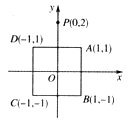
A. (0,2) B. (2,0) C. (0,-2) D. (-2,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线与x轴交于A,B两点,与y轴交于C点,点A的坐标为(2,0),点C的坐标为(0,3),它的对称轴是直线x=-![]() .
.
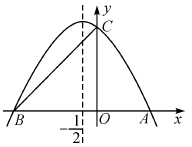
(1)求抛物线的解析式;
(2)M是线段AB上的任意一点,当△MBC为等腰三角形时,求M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某饮料瓶上有这样的字样:Eatable Date 18 months.如果用x(单位:月)表示Eatable Date(保质期),那么该饮料的保质期可以用不等式表示为__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com