
【题目】如图,抛物线与x轴交于A,B两点,与y轴交于C点,点A的坐标为(2,0),点C的坐标为(0,3),它的对称轴是直线x=-![]() .
.
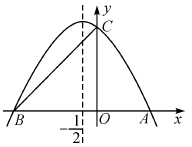
(1)求抛物线的解析式;
(2)M是线段AB上的任意一点,当△MBC为等腰三角形时,求M点的坐标.
【答案】(1)、y=![]() ;(2)、(0,0)或(3
;(2)、(0,0)或(3![]() -3,0)
-3,0)
【解析】
试题分析:(1)、首先将抛物线的解析式设成顶点式,然后将A、C两点坐标代入进行计算;(2)、首先求出点B的坐标,然后分三种情况进行计算.
试题解析:(1)依题意,设抛物线的解析式为y=a![]() +k.由A(2,0),C(0,3)得
+k.由A(2,0),C(0,3)得
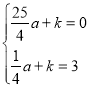 解得
解得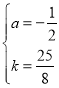 ∴抛物线的解析式为y=
∴抛物线的解析式为y=![]() .
.
(2)当y=0时,有![]() =0. 解得x1=2,x2=-3.∴B(-3,0).
=0. 解得x1=2,x2=-3.∴B(-3,0).
∵△MBC为等腰三角形,则
①当BC=CM时,M在线段BA的延长线上,不符合题意.即此时点M不存在;
②当CM=BM时,∵M在线段AB上,∴M点在原点O上.即M点坐标为(0,0);
③当BC=BM时,在Rt△BOC中,BO=CO=3,由勾股定理得BC=![]() =3
=3![]() ,∴BM=3
,∴BM=3![]() .
.
∴M点坐标为(3![]() -3,0).
-3,0).
综上所述,M点的坐标为(0,0)或(3![]() -3,0).
-3,0).


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】在校阳光运动会比赛中,某同学在投掷实心球时,实心球出手(点A处)的高度是1.4m,出手后的实心球沿一段抛物线运行,当运行到最大高度y=2m时,水平距离x=3m.

(1)试求实心球运行高度y与水平距离x之间的函数关系式;
(2)设实心球落地点为C,求此次实心球被推出的水平距离OC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙![]() 是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙
是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙![]() 于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF。
于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF。
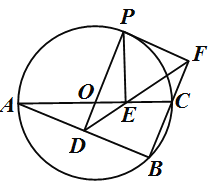
(1)、若∠POC=60°,AC=12,求劣弧PC的长;(结果保留π)
(2)、求证:OD=OE;
(3)、求证:PF是⊙![]() 的切线。
的切线。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
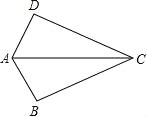
A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com