
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.![]() 是边
是边![]() 的中点,联结
的中点,联结![]() 、
、![]() ,且
,且![]() .设
.设![]() ,
,![]() .
.


(1)如果![]() ,求
,求![]() 的长;
的长;
(2)求![]() 关于
关于![]() 的函数解析式,并写出自变量
的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
(3)联结![]() .如果
.如果![]() 是以边
是以边![]() 为腰的等腰三角形,求
为腰的等腰三角形,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ,自变量
,自变量![]() 的取值范围是
的取值范围是![]() ,且
,且![]() ;(3)
;(3)![]()
【解析】
(1)首先过点D作DH⊥BC,垂足为点H,由AD∥BC,AB⊥BC,DH⊥BC,可求得DH的长,然后设CH=![]() ,则CD=2
,则CD=2![]() ,利用勾股定理即可求得答案;
,利用勾股定理即可求得答案;
(2)首先取CD的中点F,连接EF,由梯形的中位线,可表示出EF的长,易得四边形ABHD是平行四边形,然后由勾股定理可求得答案;
(3)分别从CD=BD或CD=BC去分析求解即可求得答案.
(1)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .
.
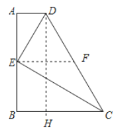
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
在![]() 中,
中,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
设![]() ,则
,则![]() ,
,
利用勾股定理,得![]() .
.
即得![]() ,
,
解得![]() (负值舍去).
(负值舍去).
∴![]() ;
;
(2)取CD的中点F,连接EF,

∵![]() 为边
为边![]() 的中点,
的中点,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
由![]() ,
,![]() ,得
,得![]() .
.
∴![]() .
.
又∵![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
即得![]() ,
,
在![]() 中,利用勾股定理,得
中,利用勾股定理,得![]() .
.
即得![]() .
.
解得![]() .
.
∴所求函数解析式为![]() .
.
自变量![]() 的取值范围是
的取值范围是![]() ,且
,且![]() .
.
(3)当![]() 是以边
是以边![]() 为腰的等腰三角形时,有两种可能情况:
为腰的等腰三角形时,有两种可能情况:
![]() 或
或![]() .
.
①如果![]() ,
,
作![]() 于H,
于H,
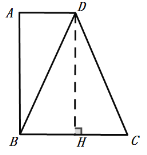
∴![]() ,
,
即得![]() ,
,
∵![]() ,
,
∴![]() .
.
解得![]() ,
,![]() .
.
经检验:![]() ,
,![]() ,是方程的解,
,是方程的解,
但![]() 不合题意,舍去.
不合题意,舍去.
∴![]() ;
;
②如果![]() ,则
,则![]() .
.
即得![]() (不合题意,舍去).
(不合题意,舍去).
综上,如果![]() 是以边
是以边![]() 为腰的等腰三角形,
为腰的等腰三角形,![]() 的值为
的值为![]() .
.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连接CF.
(1)求证:AD⊥CF;
(2)连接AF,试判断△ACF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.圆内接正六边形的边长与该圆的半径相等
B.在平面直角坐标系中,不同的坐标可以表示同一点
C.一元二次方程ax2+bx+c=0(a≠0)一定有实数根
D.将△ABC绕A点按顺时针方向旋转60°得△ADE,则△ABC与△ADE不全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AC、BD交于点O,点P、E分别是直线BD、BC上的动点,且PE=PC,过点E作EF∥AC交直线BD于点F.


(1)如图1,当∠COD=90°时,判断△BEF的形状,并说明理由;
(2)如图2,当点P在线段BO上时,求证:OP=BF;
(3)当∠COD=60°,CD=3时,请直接写出当△PEF成为直角三角形时的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值.
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.
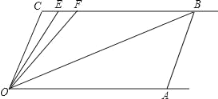
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,一张四边形纸片ABCD,∠A=50°,∠C=150°.若将其按照图②所示方式折叠后,恰好MD′∥AB,ND′∥BC,则∠D的度数为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com