
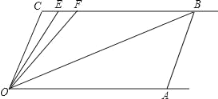
����Ŀ����ͼ��ֱ��CB��OA����C����OAB��100����E��F��CB�ϣ��������FOB����AOB��OEƽ�֡�COF
��1�����EOB�Ķ�����
��2����ƽ���ƶ�AB����ô��OBC����OFC��ֵ�Ƿ���֮�����仯�����仯���ҳ��仯���ɻ�����仯��Χ�������䣬��������ֵ��
��3����ƽ���ƶ�AB�Ĺ����У��Ƿ����ij�������ʹ��OEC����OBA�������ڣ������������������ڣ�˵�����ɣ�
���𰸡���1��40������2����OBC����OFC��1��2���Ƕ�ֵ����3��60��
��������
��1��������ֱ��ƽ�У�ͬ���ڽǻ��������AOC��Ȼ�������EOB��![]() ��AOC�����㼴�ɵý⣻
��AOC�����㼴�ɵý⣻
��2��������ֱ��ƽ�У��ڴ�����ȿɵá�AOB����OBC���ٸ��������ε�һ����ǵ������������ڵ������ڽǵĺͿɵá�OFC��2��OBC���Ӷ��ý⣻
��3�����������ε��ڽǺͶ��������COE����AOB���Ӷ��õ�OB��OE��OF�ǡ�AOC���ĵȷ��ߣ������������ε��ڽǺͶ�����ʽ���㼴�ɵý⣮
�⣺��1����CB��OA��
���AOC��180������C��180����100����80����
��OEƽ�֡�COF��
���COE����EOF��
�ߡ�FOB����AOB��
���EOB����EOF+��FOB��![]() ��AOC��
��AOC��![]() ��80����40����
��80����40����
��2����CB��OA��
���AOB����OBC��
�ߡ�FOB����AOB��
���FOB����OBC��
���OFC����FOB+��OBC��2��OBC��
���OBC����OFC��1��2���Ƕ�ֵ��
��3������COE����AOB��
�ߡ�OEC����OBA����C����OAB��
���COE����AOB��
��OB��OE��OF�ǡ�AOC���ĵȷ��ߣ�
���COE��![]() ��AOC��
��AOC��![]() ��80����20����
��80����20����
���OEC��180������C����COE��180����100����20����60����
�ʴ���ij�������ʹ��OEC����OBA����ʱ��OEC����OBA��60����


 ��������ϵ�д�
��������ϵ�д� ��ӡ�Ļ���ʱ����ϵ�д�
��ӡ�Ļ���ʱ����ϵ�д� ��ѧ�����ϵ�д�
��ѧ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��G���߶�AB��һ�㣬AC��DG�ཻ�ڵ�E��
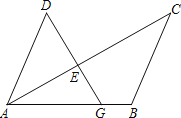
��1������������ABC��ƽ����BF����AC�ڵ�F�����߹���ͼ��������ͼ�ۼ�����д������֤����
��2��Ȼ��֤������AD��BC��AD��BC����ABC��2��ADGʱ��DE��BF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() �DZ�
�DZ�![]() ���е㣬����
���е㣬����![]() ��
��![]() ����
����![]() ����
����![]() ��
��![]() ��
��


��1�����![]() ����
����![]() �ij���
�ij���
��2����![]() ����
����![]() �ĺ�������ʽ����д���Ա���
�ĺ�������ʽ����д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3������![]() �����
�����![]() ���Ա�
���Ա�![]() Ϊ���ĵ��������Σ���
Ϊ���ĵ��������Σ���![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������A1B1C1D1E1F1�ı߳�Ϊ1�����������Խ�����Χ��һ����������A2B2C2D2E2F2 �� ��˼�����ȥ������������A4B4C4D4E4F4������� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
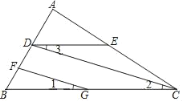
����Ŀ����������֤��
��1����ͼ��FG��CD����1����3����B��50�������BDE�Ķ�����
�⣺��FG��CD����֪��
���2���� ��
�֡ߡ�1����3��
���3����2������������
��BC���� ��
���B+�� ����180���� ��
�֡ߡ�B��50��
���BDE���� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
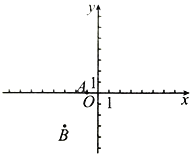
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�A��-1��0����B��-3��-3������BC��OA����BC=4OA.
��1�����C�����ꣻ
��2������ABC�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������У�ÿ��С�����εı߳���Ϊ1����λ���ȣ���ABC�����������λ����ͼ��ʾ.�ֽ���ABCƽ�ƣ�ʹ��A�任Ϊ��D����E��F�ֱ���B��C�Ķ�Ӧ��.
(1)�뻭��ƽ�ƺ����DEF��������DEF�������
(2)������AD��CF�����������߶�֮��Ĺ�ϵ��________________ .

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����нⷽ����ķ������ش����⣮
�ⷽ����![]()
�⣺�ɢ٩��ڵ�2x+2y=2��x+y=1��
����16��16x+16y=16��
�ک��ܵ�x=��1���Ӷ��ɵ�y=2
��ԭ������Ľ���![]()
��1�������������Ľⷨ�ⷽ����![]() ��
��
��2����²����x��y�ķ�����![]()
�Ľ���ʲô�������÷�����Ľ������֤��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����ǰ���ͼ���ã����� ![]() ��
�� ![]() ��б��AB=6cm,DC=7cm�����ǰ�DCE�Ƶ�C˳ʱ����ת15��õ���D1CE1����ͼ�ң�����ʱAB��CD1�ཻ�ڵ�O����D1E1�ཻ�ڵ�F ��
��б��AB=6cm,DC=7cm�����ǰ�DCE�Ƶ�C˳ʱ����ת15��õ���D1CE1����ͼ�ң�����ʱAB��CD1�ཻ�ڵ�O����D1E1�ཻ�ڵ�F �� 
��1���� ![]() �Ķ�����
�Ķ�����
��2�����߶�AD1�ij���
��3������������D1CE1���ŵ� C ˳ʱ������ת30��á�D2CE2 �� ��ʱ��B�ڡ�D2CE2���ڲ����ⲿ�����DZ��ϣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com