
分析 (1)根据判别式的意义得到△=(2k-3)2-4(k2+1)≥0,然后解不等式即可;
(2)根据根与系数的关系得到x1+x2=2k-3,x1•x2=k2+1>0,则可判断x1、x2同号,然后去绝对值,当x1+x2=3,即2k-3=3;当-(x1+x2)=3,即-(2k-3)=3,然后分别解关于k的方程即可.
解答 解:(1)若方程有实数根,
则△=(2k-3)2-4(k2+1)≥0,
∴k≤$\frac{5}{12}$
∴当k≤$\frac{5}{12}$时,此方程有实数根;
(2)根据题意得x1+x2=2k-3,x1•x2=k2+1>0,
则x1、x2同号,
当x1>0,x2>0,则x1+x2=3,即2k-3=3,解得k=3,
当k=3时,原方程无实数根,舍去,
当x1<0,x2<0,则-(x1+x2)=3,即-(2k-3)=3,解得k=0,
即k的值为0.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.


科目:初中数学 来源: 题型:解答题
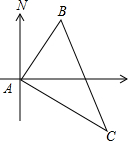 甲、乙两船同时从A码头开出,45分钟后,甲船到达B码头,乙船到达C码头,这时两船相距15海里;已知甲船航行的速度是12海里/时.乙船航行的速度是16海里/时,甲船航行的方向是北偏东40°,求乙船航行的方向.
甲、乙两船同时从A码头开出,45分钟后,甲船到达B码头,乙船到达C码头,这时两船相距15海里;已知甲船航行的速度是12海里/时.乙船航行的速度是16海里/时,甲船航行的方向是北偏东40°,求乙船航行的方向.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
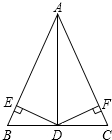 如图,在△ABC中,AB=AC,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF.请选择一对你认为全等的三角形并加以证明.
如图,在△ABC中,AB=AC,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF.请选择一对你认为全等的三角形并加以证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
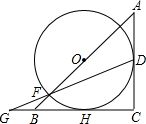 如图,在等腰直角三角形ABC中,以斜边AB的中点O为圆心的⊙O与AC相切于点D,与AB相交于点E,F,DF与CB的延长线交于点G.
如图,在等腰直角三角形ABC中,以斜边AB的中点O为圆心的⊙O与AC相切于点D,与AB相交于点E,F,DF与CB的延长线交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
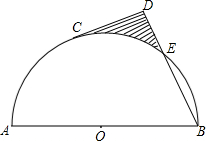 如图,点C在半圆0上,直径AB=8,$\widehat{BC}$=2$\widehat{AC}$,过点C作切线CD,BD⊥CD,则阴影部分的面积是( )
如图,点C在半圆0上,直径AB=8,$\widehat{BC}$=2$\widehat{AC}$,过点C作切线CD,BD⊥CD,则阴影部分的面积是( )| A. | 8$\sqrt{3}$-4π | B. | 8$\sqrt{3}$-$\frac{8}{3}$π | C. | 4π-6$\sqrt{3}$ | D. | 6$\sqrt{3}$-$\frac{8}{3}$π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
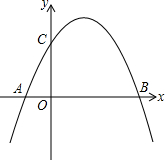 如图,抛物线y=-x2+bx+c与x轴交于AB两点(A在B的左侧),与y轴相交于点C(0,3),抛物线的顶点在第一象限,AB=4.
如图,抛物线y=-x2+bx+c与x轴交于AB两点(A在B的左侧),与y轴相交于点C(0,3),抛物线的顶点在第一象限,AB=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com