
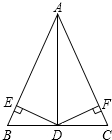
 如图,在△ABC中,AB=AC,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF.请选择一对你认为全等的三角形并加以证明.
如图,在△ABC中,AB=AC,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF.请选择一对你认为全等的三角形并加以证明.分析 (1)结合等腰三角形的性质以及角平分线的性质即可找出三对全等的三角形,在中间任选一对加以证明;
(2)由“DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF”可得知DA为∠BAC的角平分线,即得出∠BAD=∠CAD,结合已知条件及公共边AD,可用全等三角形的判定定理SAS证出△BAD≌CAD.
解答 解:(1)题中给定的全等三角形有三对:△BAD≌CAD,△EAD≌△FAD,△BED≌CFD,
选第一对全等三角形来证明.
故答案为:BAD;CAD.
(2)证明:∵DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF,
∴DA为∠BAC的角平分线,
∴∠BAD=∠CAD.
在△BAD和△CAD中,有$\left\{\begin{array}{l}{BA=CA}\\{∠BAD=∠CAD}\\{AD=AD}\end{array}\right.$,
∴△BAD≌CAD(SAS).
点评 本题考查了全等三角形的判定、等腰三角形的性质以及角平分线的性质,解题的关键是:(1)结合已知找出3对全等的三角形;(2)找出满足SAS的相等的边角.本题属于基础题,难度不大,解决该题型题目时,根据等腰三角形的性质找出相等的边角关系是关键.


科目:初中数学 来源: 题型:解答题
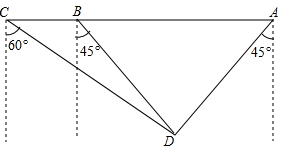 如图,某海监船向正西方向航行,在A处望见一艘正在作业渔船D在南偏西45°方向上,海监船航行到B处时望见渔船D在南偏东45°方向上,又航行了半小时到达C处,望见渔船D在南偏东60°方向上,若海监船的速度为40海里/时,求A,B之间的距离.(结果保留根号)
如图,某海监船向正西方向航行,在A处望见一艘正在作业渔船D在南偏西45°方向上,海监船航行到B处时望见渔船D在南偏东45°方向上,又航行了半小时到达C处,望见渔船D在南偏东60°方向上,若海监船的速度为40海里/时,求A,B之间的距离.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
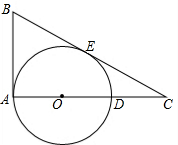 如图,在Rt△ABC中,∠BAC=90°,点O在AC上,BC切⊙O于点E,且AB=5,AC=12.
如图,在Rt△ABC中,∠BAC=90°,点O在AC上,BC切⊙O于点E,且AB=5,AC=12.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲、乙都正确 | B. | 甲正确,乙不正确 | C. | 甲、乙都不正确 | D. | 乙正确,甲不正确 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
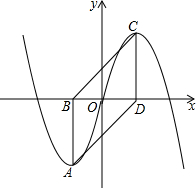 如图,在平面直角坐标系中,过抛物线y=a(x+1)2-2(x≤0,a为常数)的顶点A作AB⊥x轴于点B,过抛物线y=-a(x-1)2+2(x≥0,a为常数)的顶点C作CD⊥x轴于点D,连结AD、BC.则四边形ABCD的面积为4.
如图,在平面直角坐标系中,过抛物线y=a(x+1)2-2(x≤0,a为常数)的顶点A作AB⊥x轴于点B,过抛物线y=-a(x-1)2+2(x≥0,a为常数)的顶点C作CD⊥x轴于点D,连结AD、BC.则四边形ABCD的面积为4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com