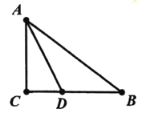
【题目】如图，在
中，
，
是的角平分线．若
，
，则
____________．
【答案】3
【解析】
过点D作DE⊥AB于E，根据角平分线上的点到角的两边的距离相等可得CD=DE，然后利用“HL”证明△ACD和△AED全等，根据全等三角形对应边相等可得AE=AC，表示出BE，设DE=x，表示出BD，然后利用勾股定理列式计算即可得解．
如图，过点D作DE⊥AB于E，
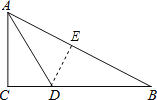
∵AC=6，BC=8，
∴AB=
=10，
∵∠C=90°，AD是∠BAC的角平分线，
∴CD=DE，
在△ACD和△AED中，
，
∴△ACD≌△AED（HL），
∴AE=AC=6，
BE=AB-AE=10-6=4，
设DE=x，
则BD=8-x，
在Rt△BDE中，DE2+BE2=BD2，
∴x2+42=（8-x）2，
解得x=3，即DE=3．
AD=
=3 .
故答案为：3 .
阳光课堂课时作业系列答案科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，一次函数 y=nx+2(n≠0)的图像与反比例函数 y 
(m≠0)在第一象限内的图像交于点 A，与 x 轴交于点 B，线段 OA=5，C 为 x 轴正半轴上一点，且 sin AOC 
.
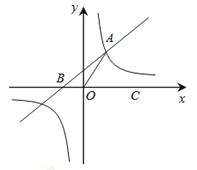
(1)求一次函数和反比例函数的解析式；
(2)求△ AOB 的面积；
(3)请直接写出不等式 nx 2 的解.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD中，∠A＝90°，AB＝12，AD＝5，点M、N分别为线段BC、AB上的动点（含端点，但点M不与点B重合），点E、F分别为DM、MN的中点，则EF长度的可能为（ ）
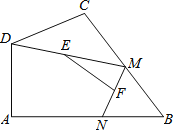
A.2B.5C.7D.9
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：如图，点M，N把线段AB分割成AM.MN，NB，若以AM，MN，NB为边的三角形是一个直角三角形，则称点M、N是线段AB的勾股分割点.
（1）已知M、N线段AB分割成AM，MN，NB，若
，则点M，N是线段AB的勾股分割点吗？请说明理由；
（2）已知点M、N是线段AB的勾股分割点，且AM为直角边，若
，求BN的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我市2013年体育中考考试方案公布后，同学们将根据自己平的运动成绩确定自己的报考项目，下面是小亮同学近期在两个项目中连续五次测试的（得分情况得分统计表得分折线图）
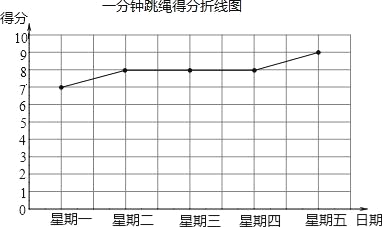
立定跳远测试日期 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
得分 | 7 | 10 | 8 | 9 | 6 |
（1）请根据图表信息，分别计算小亮这两个项目测试成绩的平均数和方差；
（2）根据以上信息，你认为在立定跳远和一分钟跳绳这两个项目中，小亮应选择哪个项目作为体育考试的报考项目？并简述理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了了解学生学习的环境（教室），研究人员对某校一间（坐满学生、门窗关闭）教室中的
的总量进行检测，得到的部分数据如下：
教室连续使用时间 |
|
|
|
|
|
|
|
|
|
|
|
经研究发现，该教室空气中总量
是教室连使用时间
的一次函数．
（1）请直接写出
与的函数关系式；
（2）根据有关资料推算，当该教室空气中总量达到
时，学生将会稍感不适，则该教室连续使用__________
学生将会开始稍感不适．
（3）如果该教室在连续使用
分钟时开门通风，在学生全部离开教室的情况下，
分钟可将教室空气中的总量减少到
，求开门通风时教室空气中平均每分钟减少多少立方米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，边长为1的正方形ABCD的对角线交于点O，点E是边AB上一动点，点F在边BC上，且满足OE⊥OF，在点E由A运动到B的过程中，以下结论正确的个数为( )
①线段OE的大小先变小后变大；②线段EF的大小先变大后变小；③四边形OEBF的面积先变大后变小．
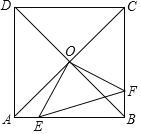
A.0B.1C.2D.3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数y1=kx+b的图象与反比例函数
的图象交于点A（﹣2，﹣5），C（5，n），交y轴于点B，交x轴于点D．
（1）求反比例函数
和一次函数y1=kx+b的表达式；
（2）连接OA，OC，求△AOC的面积；
（3）根据图象，直接写出y1＞y2时x的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
