
分析 (1)先根据二次根式的性质求出a的范围,然后去掉绝对值号进行化简.最后利用非负性求出a+b的值
(2)先将a+b+|$\sqrt{c-1}$-1|=4$\sqrt{a-2}$+2$\sqrt{b+1}$-4,化为几个非负数的和为零的形式,然后利用非负性求出a、b、c的值.
解答 (1)解:∵$\sqrt{a-4}$
∴a-4≥0
∴$({a-4})+{({b+3})^2}+\sqrt{a-4}+4=a$
∴${({b+3})^2}+\sqrt{a-4}=0$
∴b+3=0,a-4=0
∴b=-3,a=4
∴a+b=1
(2)由题意可知:$a+b+|{\sqrt{c-1}-1}|-4\sqrt{a-2}-2\sqrt{b+1}+4=0$
∴$({a-2})-4\sqrt{a-2}+4+({b+1})-2\sqrt{b+1}+1+|{\sqrt{c-1}-1}|=0$
${({\sqrt{a-2}-2})^2}+{({\sqrt{b+1}-1})^2}+|{\sqrt{c-1}-1}|=0$
∴$\sqrt{a-2}=2$,$\sqrt{b+1}=1$,$\sqrt{c-1}=1$
∴a=6,b=0,c=2
∴a+2b-2c=6+0-2×2=2
点评 本题考查非负数的性质,解题的关键是将所给的式子化为非负数的和为0的性质,然后利用非负性求出a、b、c的值,本题属于中等题型.


科目:初中数学 来源: 题型:解答题
 应用一元二次方程解答下列问题:
应用一元二次方程解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | $\frac{18}{13}$ | D. | $\frac{60}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
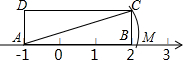 如图,四边形ABCD是矩形,BC=1,则点M表示的数是( )
如图,四边形ABCD是矩形,BC=1,则点M表示的数是( )| A. | 2 | B. | $\sqrt{5}-1$ | C. | $\sqrt{5}$ | D. | $\sqrt{10}-1$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A | B | |
| 成本(元/件) | 120 | 85 |
| 利润(元/件) | 60 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com