
分析 将y=1和y=2分别代入y=$\frac{1}{x}$、y=$\frac{2}{x}$中求出点A1、B1、B2、A2的坐标,由此即可求出线段A1B1、A2B2的长度,再根据梯形的面积公式即可得出四边形A1B1B2A2的面积,同理可求出四边形AnBnBn+1An+1的面积.
解答 解:∵直线y=1与双曲线y=$\frac{1}{x}$相交于点A1,与双曲线y=$\frac{2}{x}$相交于点B1,直线y=2与双曲线y=$\frac{1}{x}$相交于点A2,与双曲线y=$\frac{2}{x}$相交于点B2,
∴A1(1,1),B1(2,1),A2($\frac{1}{2}$,2),B2(1,2).
∴A1B1=2-1=1,A2B2=1-$\frac{1}{2}$=$\frac{1}{2}$.
∵直线y=1与直线y=2平行,
∴四边形A1B1B2A2为梯形,
∴四边形A1B1B2A2的面积=$\frac{1}{2}$(A1B1+A2B2)×(2-1)=$\frac{1}{2}$×(1+$\frac{1}{2}$)×1=$\frac{3}{4}$.
∵直线y=n与双曲线y=$\frac{1}{x}$相交于点An,与双虚线y=$\frac{2}{x}$相交于点Bn,直线y=n+1与双曲线y=$\frac{1}{x}$相交于点An+1,与双曲线y=$\frac{2}{x}$相交于点Bn+1,
∴An($\frac{1}{n}$,n),Bn,($\frac{2}{n}$,n),An+1($\frac{1}{n+1}$,n+1),Bn+1($\frac{2}{n+1}$,n+1),
∴AnBn=$\frac{2}{n}$-$\frac{1}{n}$=$\frac{1}{n}$,An+1Bn+1=$\frac{2}{n+1}$-$\frac{1}{n+1}$=$\frac{1}{n+1}$.
∵直线y=n与直线y=n+1平行,
∴四边形AnBnBn+1An+1为梯形,
∴四边形AnBnBn+1An+1的面积=$\frac{1}{2}$(AnBn+An+1Bn+1)×(n+1-n)=$\frac{1}{2}$×($\frac{1}{n}$+$\frac{1}{n+1}$)×1=$\frac{2n+1}{2n(n+1)}$.
故答案为:$\frac{3}{4}$;$\frac{2n+1}{2n(n+1)}$.
点评 本题考查了反比例函数与一次函数的交点问题、梯形以及两点间的距离公式,熟练掌握梯形的面积公式是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB为半圆O的直径,AD、BC分别切⊙O于A,B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2,④OD:OC=DE:OE,⑤OD2=DE•CD,正确的有( )
如图,AB为半圆O的直径,AD、BC分别切⊙O于A,B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2,④OD:OC=DE:OE,⑤OD2=DE•CD,正确的有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
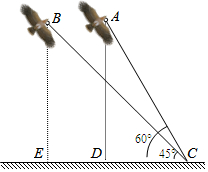 在一个阳光明媚、清风徐来的周末,小明和小强一起到郊外放风筝﹒他们把风筝放飞后,将两个风筝的引线一端都固定在地面上的C处(如图).现已知风筝A的引线(线段AC)长20m,风筝B的引线(线段BC)长24m,在C处测得风筝A的仰角为60°,风筝B的仰角为45°.
在一个阳光明媚、清风徐来的周末,小明和小强一起到郊外放风筝﹒他们把风筝放飞后,将两个风筝的引线一端都固定在地面上的C处(如图).现已知风筝A的引线(线段AC)长20m,风筝B的引线(线段BC)长24m,在C处测得风筝A的仰角为60°,风筝B的仰角为45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com