Question

17．如图1，在平面直角坐标系中，直线y=x+6与x轴交于点A，与y轴交于点B．

①如图2，若过点B作直线BC使得BC⊥AB于点B，且交x轴于C，求△ABC的面积．
②D为线段OA延长线上一动点，在第二象限内以BD为直角边做等腰直角三角形BDE，连结EA．求直线EA的函数表达式．
③如图3，点F是y轴正半轴上一点，且F点坐标为（0，2$\sqrt{3}$），AG平分∠OAF，点M是射线AG上一动点，点N是线段AO上一动点，试判断是否存在这样的点M、N，使得OM+MN的值最小？若存在，请写出其最小值，并加以说明．

Answer 1

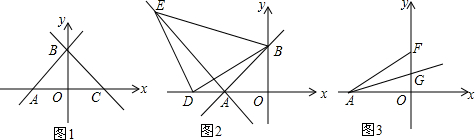
分析 ①根据直线与坐标轴的交点易得A，B两点坐标，然后根据三角形面积公式计算；
②过点E作x轴的垂线EM交x轴点M，根据全等三角形的判定和直线解析式的解答即可；
③根据勾股定理进行解答即可．

解答 解：①由题意可得：A点坐标为（-6，0），B点坐标为（0，6），
则△AOB为等腰直角三角形，
∵BC⊥AB，
∴△ABC为等腰直角三角形且AC=12，
∴S_△ABC=36；
②过点E作x轴的垂线EM交x轴点M，如图1：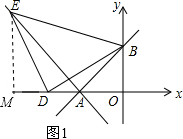
．
设线段DA=a，则DO=6+a，
∵△EDB为等腰直角三角形，
∴ED=DB且∠EDB=90°，
∴∠EDM+∠BDO=90°，
易得：∠EDM=∠DBO，∠EMD=∠BOB=90°，
∴△EMD≌△DOB，
∴EM=DO=6+a，MD=BO=6，
$\begin{array}{l}∵点M，D在x轴负半轴上，点E在第二象限内\\∴点E的坐标为（-12-a，6+a）\end{array}$
设经过A，E两点的直线解析式为y=kx+b则有：
$\left\{\begin{array}{l}-6k+b=0\\（-12-a）k+b=6+a\end{array}\right.$
解得：$\left\{\begin{array}{l}{k=-1}\\{b=-6}\end{array}\right.$，
直线EA的解析式为y=-x+6；
③线段AO，射线AG上分别任取点N，M作点N关于射线AG对称的点N'，由题意可知点N'落在AF上，要使得OM+MN的值最小则需要点O，M，N'三点共线且ON'⊥AF，如图2：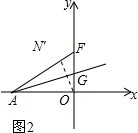

由勾股定理得$AF=4\sqrt{3}$，
${S_{△AOE}}=\frac{1}{2}AO*OF=\frac{1}{2}AF*ON'$
则有：ON'=3，
因此OM+MN的最小值为3．

点评 本题考查了一次函数的综合题，关键是根据直线与坐标轴的交点易得A，B两点坐标进行解答．