
分析 (1)根据小丽的操作步骤可以得到问题的答案;
(2)根据小明的操作步骤可以得到问题的答案;
(3)根据第一问中小丽的操作步骤可以设计出相应的方案;
(4)根据小明的操作步骤可以得到问题的答案.
解答 解:(1)根据题意可得,A型纸片1张,B型纸片3张,C型纸片2张,
∴(a+b)(a+2b)=a2+3ab+2b2.
故答案为:a2+3ab+2b2.
(2)根据题意可得,a2+5ab+6b2=(a+2b)(a+3b).
故答案为:(a+2b)(a+3b).
(3)计算(a+b)3
操作步骤如下:
①准备若干块A、B、C型纸片,其中A型纸片是边长为a的正方形,B型纸片是边长分别为a、b的长方形,C型纸片是边长为b的正方形;
②用①中的纸片拼成棱长为a+b的正方体;
③数出以a为棱长的正方体一个,以a为边长的正方形做底面,高为b的长方体三个,以b为边长的正方形做底面,高为a的长方体三个,以b为棱长的正方体一个,得(a+b)3=a3+3a2b+3ab2+b3.
(4)分解因式a3+6a2b+12ab2+8b3
根据小明的操作步骤可得,a3+6a2b+12ab2+8b3=(a+2b)3.
点评 本题考查解因式分解的应用,解题的关键是能看懂小丽和小明的操作步骤,在(3)和(4)中可以与长方体和正方体联系在一起.


 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:选择题
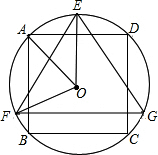 如图,△EFG是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥FG,则∠AOF的度数是( )
如图,△EFG是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥FG,则∠AOF的度数是( )| A. | 60° | B. | 65° | C. | 72° | D. | 75° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com