
����Ŀ�������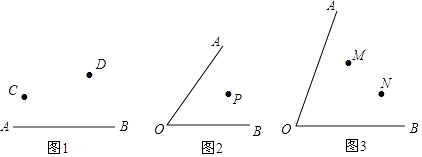
��1����ͼ1����ABֱ��һ��C��D���㣬��AB����һ��P��ʹC��D��P������ɵ������ε��ܳ���̣��ҳ��˵㲢˵�����ɣ�
��2����ͼ2���ڡ�AOB�ڲ���һ��P���Ƿ���OA��OB�Ϸֱ���ڵ�E��F��ʹ��E��F��P������ɵ������ε��ܳ���̣��ҳ�E��F���㣬��˵�����ɣ�
��3����ͼ3���ڡ�AOB�ڲ�������M��N���Ƿ���OA��OB�Ϸֱ���ڵ�E��F��ʹ��E��F��M��N���ĵ���ɵ��ı��ε��ܳ���̣��ҳ�E��F���㣬��˵�����ɣ�
���𰸡�
��1��
�⣺��ͼ1����C����ֱ��AB�ĶԳƵ�C�䣬
����C��D��AB�ڵ�P��
���P������Ҫ�����ĵ㣮
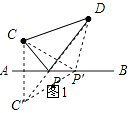
���ɣ���l��ȡ��ͬ��P�ĵ�P�䣬����CP�䡢DP�䣮
��C��C�����ֱ��l�Գƣ�
��PC=PC�䣬P��C=P��C�䣬
��C��P+DP��C��P��+DP�䣬
��PC+DP��CP��+DP��
��CD+CP+DP��CD+CP��+DP��
����CDP�ܳ�С�ڡ�CDP���ܳ�
��2��
�⣺��ͼ2����P����OA�ĶԳƵ�C������OB�ĶԳƵ�D������CD����OA��E��OB��F��
���E��F������Ҫ�����ĵ㣮

���ɣ���OA��OB��ȡ��ͬ��E��F�ĵ�E�䣬F�䣬����CE�䡢E��P�䣬
��C��P����ֱ��OA�Գƣ�
��PE=CE��CE��=PE�䣬PF=DF��PF��=DF�䣬
��PE+EF+PF=CE+EF+DF��PE��+PF��+E��F��=CE��+E��F��+DE�䣬
��CE+EF+DF��CE��+E��F��+DF�䣬��
��PE+EF+PF��PE��+PF��+E��F��
��3��
�⣺��ͼ3����M����OA�ĶԳƵ�C������OB�ĶԳƵ�D������CD����OA��E��OB��F��
���E��F������Ҫ�����ĵ㣮

���ɣ���OA��OB��ȡ��ͬ��E��F�ĵ�E�䣬F�䣬����CE�䡢E��P�䣬
��C��P����ֱ��OA�Գƣ�
��PE=CE��CE��=PE�䣬PF=DF��PF��=DF�䣬
�ɣ�2����֪MN+ME+EF+MF��ME��+E��F��+F��D��
����������1�����ڡ�PCD���ܳ�=PC+CD+PD����CD�Ƕ�ֵ����ֻ����ֱ��l����һ��P��ʹPC+PD��С�������C����l�ĶԳƵ�ΪC�䣬ʹPC+PD��С����ʹPC��+PD��С����2����P����OA��OB�ĶԳƵ�C��D������CD��OA��OB��E��F����ʱ��PEF�ܳ�����Сֵ����3����ͼ3����M����OA�ĶԳƵ�C������OB�ĶԳƵ�D������CD����OA��E��OB��F����ʱʹ��E��F��M��N���ĵ���ɵ��ı��ε��ܳ���̣�
�����㾫�����������⣬������Ҫ�˽���ԳƵ�����(����ij��ֱ�߶ԳƵ�����ͼ����ȫ���Σ��������ͼ�ι���ijֱ�߶Գƣ���ô�Գ����Ƕ�Ӧ�����ߵĴ�ֱƽ���ߣ�����ͼ�ι���ijֱ�߶Գƣ�������ǵĶ�Ӧ�߶λ��ӳ����ཻ����ô�����ڶԳ�����)����Ҫ������Գ�-���·������(��֪����㣬�����·������ȷ������෴����֪�յ��㣬�����·������֪�����յ㣬�������֮������·������ͼ���������·��)�����֪ʶ���Ǵ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪��ABC���������������ֱ�ΪA����2��3����B����6��0����C����1��0����

��1����ֱ��д����B���ڵ�A�ԳƵĵ�����ꣻ
��2������ABC������ԭ��O��ʱ����ת90��������ͼ�Σ�ֱ��д����B�Ķ�Ӧ������ꣻ
��3����ֱ��д������A��B��CΪ�����ƽ���ı��εĵ��ĸ�����D�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��·��һ·�εĵ�·ά�����������б꣬���мס����������̶Ӿ��꣬������������ʾ�����̶ӵ�����ɴ������Ҫ10�죬�ҹ��̶ӵ�����ɴ������Ҫ15�죬�����̶�ÿ��Ĺ��̷��ñ��ҹ��̶Ӷ�300Ԫ���ס������Ӻ�������Ҫ10200Ԫ������ָ�ӶӾ����Ӽס����������̶���ѡһ�ӵ�����ɣ����ӽ�ʡ�ʽ�ĽǶȿ��ǣ�Ӧѡ�ĸ����̶ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ��ѧ��Ϊ�˶�С�����л�������ʶ������ʦ�Ĵ����¶�С���������˲����������������£���ͼ����Ӳ��С�����ز���D��������һ��E�ľ���Ϊ115.2�ף�С�����Ķ���Ϊ��B����BD��DE���ڵ�E����ֱ��һ��ľ�����䶥��ΪC��CE=1.72�ף���DE���ӳ�������һ��A��ʹA��C��B������ͬһֱ���ϣ����AE=4.8�ף���С�����ĸ߶ȣ� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУҪ�ٰ�һ���ݽ�������ÿ��ֻ��ѡһ�˲μӱ����������꼶һ��мס������˵��ݽ�ˮƽ������£���Ҫ������������ѡһ��ȥ�μ�ȫУ���ݽ�����������������ȫ��ͬѧЭ�̾�������С�����Ϸ��ȷ��˭ȥ������ʤ�߲������� ��Ϸ�������£������������ĺ����У�һ�������������������һ��������һ�������������������һ���������������и���һ���������õ��������Ǻ���ʤ�����õ��������ǰ�����ʤ��������Ϊƽ�֣���Ϊƽ�֣�����������Ϸ��ֱ���ֳ�ʤ��Ϊֹ��
������������ش��������⣺
��1�����������Ӹ�����һ����һ����Ϊ����һ����Ϊ����ĸ����Ƕ��٣�
��2������Ϸ��ƽ�������б�����״ͼ�ȷ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
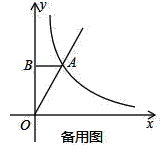
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=kx��˫����![]() �ڵ�һ�����ཻ�ڵ�A��1��2������B��y���ϣ���AB��y�ᣮ��һ����P��ԭ�������y����ÿ��1����λ���ٶ���y����������˶����˶�ʱ��Ϊt�루t��0��������P��PD��y�ᣬ��ֱ��OA�ڵ�C����˫�����ڵ�D��
�ڵ�һ�����ཻ�ڵ�A��1��2������B��y���ϣ���AB��y�ᣮ��һ����P��ԭ�������y����ÿ��1����λ���ٶ���y����������˶����˶�ʱ��Ϊt�루t��0��������P��PD��y�ᣬ��ֱ��OA�ڵ�C����˫�����ڵ�D��
��1����ֱ��y=kx��˫����![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2�����ı���CDAB�����ΪS����P���߶�OB���˶�ʱ��P����B���غϣ�����S��t֮��ĺ�����ϵʽ��
��3����ͼ�е�һ����˫�������Ƿ���ڵ�Q��ʹ��A��B��C��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ������ڣ��������ʱt��ֵ��Q������ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��
��1����A��ʾ����Ϊ ����B��ʾ����Ϊ ����C��ʾ����Ϊ ��
��2���ú�t�Ĵ���ʽ��ʾP����A�͵�C�ľ��룺 PA= ��PC= ��
��3������P�˶���B��ʱ����Q��A���������ÿ��3����λ���ٶ���C���˶���Q�㵽��C�����������ͬ�����ٶȷ��أ��˶����յ�A�����ڵ�Q���C�˶������У��ܷ��ϵ�P?���ܣ��������Q�˶������ϣ����ڵ�Q��ʼ�˶���P��Q����֮��ľ����ܷ�Ϊ2����λ������ܣ��������ʱ��P��ʾ������������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ຣ������Ѷ��2016��2��21�գ������������̵���ѹ������г�����ϵͳ��ʽ���ã�����������Ͷ����112��Ԫ������40���������г�վ�㡢����720���������г��������������Ͷ�ʣ����ڽ�����վ�㡢���ù������г���Ԥ��2018�꽫Ͷ��340.5��Ԫ���½�120���������г�վ�㡢����2205���������г���
��1������ÿ��վ�����ۺ������г��ĵ��۷ֱ��Ƕ�����Ԫ��
��2���������2016�굽2018�����������ù������г���������ƽ�������ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B��C��ͬһֱ���ϣ�HΪAC���е㣬MΪAB���е㣬NΪBC���е㣬������˵������MN=HC����MH=![]() ��AH��HB������MN=
��AH��HB������MN=![]() ��AC+HB������HN=
��AC+HB������HN=![]() ��HC+HB����������ȷ���ǣ� ��
��HC+HB����������ȷ���ǣ� ��
![]()
A���٢� B���٢ڢ� C���ڢۢ� D���٢ڢۢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com