
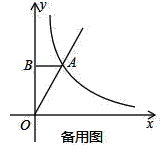
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=kx��˫����![]() �ڵ�һ�����ཻ�ڵ�A��1��2������B��y���ϣ���AB��y�ᣮ��һ����P��ԭ�������y����ÿ��1����λ���ٶ���y����������˶����˶�ʱ��Ϊt�루t��0��������P��PD��y�ᣬ��ֱ��OA�ڵ�C����˫�����ڵ�D��
�ڵ�һ�����ཻ�ڵ�A��1��2������B��y���ϣ���AB��y�ᣮ��һ����P��ԭ�������y����ÿ��1����λ���ٶ���y����������˶����˶�ʱ��Ϊt�루t��0��������P��PD��y�ᣬ��ֱ��OA�ڵ�C����˫�����ڵ�D��
��1����ֱ��y=kx��˫����![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2�����ı���CDAB�����ΪS����P���߶�OB���˶�ʱ��P����B���غϣ�����S��t֮��ĺ�����ϵʽ��
��3����ͼ�е�һ����˫�������Ƿ���ڵ�Q��ʹ��A��B��C��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ������ڣ��������ʱt��ֵ��Q������ꣻ�������ڣ���˵�����ɣ�

���𰸡���1��![]() ��
��![]() ����2��
����2��![]() ����3��
����3��![]() ʱ��Q
ʱ��Q![]() ��
��![]() ʱ��Q
ʱ��Q![]() ��
��![]() ʱ��
ʱ��![]() ��
��
��������
��1���ѵ�A������������������Ľ���ʽ���k��k����ֵ���ɵõ����������Ľ���ʽ��
��2����������AB=1��OB=2��OP=t����ϣ�1�����������������Ľ���ʽ�ɵã�PC=![]() ��PD=
��PD=![]() ��BP=
��BP=![]() ���ɴ˿ɵõ���P���߶�AB�ϣ������B�غϣ�ʱ��CD=PD-PC=
���ɴ˿ɵõ���P���߶�AB�ϣ������B�غϣ�ʱ��CD=PD-PC=![]() ������S=S����ABCD=
������S=S����ABCD=![]() ��AB+CD����BP�������S��t��ĺ�����ϵʽ�ˣ�
��AB+CD����BP�������S��t��ĺ�����ϵʽ�ˣ�
��3���������⣬����CD��AB���·���AB��CD����AB=CD����Q���D�غϣ���CD��AB�Ϸ���AB��CD����AB=CD����Q���D�غϣ���CD��AB�·���BQ��AC��BQ=AC���������������������Ӧ��ͼ�Σ�ͼ2��ͼ3�������֪�������з������.
��1����A��1��2������y=kx��y=![]() ��
��
k=2��k��=2
��ֱ��y=kx�ĺ�����ϵʽ��y=2x��˫����y=![]() �ĺ�����ϵʽ��y=
�ĺ�����ϵʽ��y=![]() ��
��
��2��������ɵ���AB=1��OB=2��OP=t��
��PC=![]() ��PD=
��PD=![]() ��BP=2-t��
��BP=2-t��
�൱CD��AB�·�ʱ��CD=PD-PC=![]() -
-![]() ��
��
��S=![]() (1+
(1+![]() -
-![]() )(2-t)=
)(2-t)= ![]() ��0��t��2����
��0��t��2����
��3����������3�����Σ��������£�
����CD��AB���·���AB��CD����AB=CD����Q���D�غ�����ͼ2��ʱ���ı���ABCQ��ƽ���ı�����
��CD=PD-PC=![]() -
-![]() =1��
=1��
��![]() �����
�����![]() ����ȥ����
����ȥ����
����ʱPD=![]() =
=![]() ��OP=t=
��OP=t=![]() -1��
-1��
�൱t=![]() -1ʱ������Q��
-1ʱ������Q��![]() ��
��![]() -1��ʹ��A��B��C��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ�
-1��ʹ��A��B��C��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ�
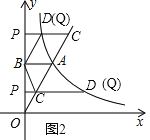
����CD��AB���Ϸ���AB��CD����AB=CD����Q���D�غ�����ͼ2��ʱ���ı���ACBQ��ƽ���ı��Σ�
��CD=PC-PD��
��![]() ����ã�
����ã�![]() ����ȥ����
����ȥ����
����ʱPD=![]() =
=![]() ��OP=t=
��OP=t=![]() +1��
+1��
�൱t=![]() +1ʱ������Q��
+1ʱ������Q��![]() ��
��![]() +1��ʹ��A��B��C��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ�
+1��ʹ��A��B��C��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ�
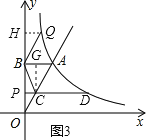
����BQ��AC��BQ=AC����CD��AB�·�ʱ����ͼ3������ʱ�ı���ACBQ��ƽ���ı��Σ�
��ʱQ���������Ϊ��![]() ��
��![]() +1����
+1����
��C��CG��AB��AB��G����Q��QH��y�ύy����H��
��֤����ACG�ա�QBH��
��CG=BH=BP����
��OP=2OB-OH=4-��![]() +1��=3-
+1��=3-![]() ��
��
�൱t=3-![]() ʱ������Q��
ʱ������Q��![]() ��
��![]() +1��ʹ��A��B��C��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ�
+1��ʹ��A��B��C��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ�


 53������ϵ�д�
53������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��y=3x��3�ֱ�x�ᡢy����A��B���㣬������y=x2+bx+c����A��B���㣬��C����������x�����һ�����㣨��A�㲻�غϣ���
��1���������ߵĽ���ʽ��
��2�����ABC�������
��3���������ߵĶԳ����ϣ��Ƿ���ڵ�M��ʹ��ABM�ܳ���̣��������ڣ���˵�����ɣ������ڣ������M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һԪһ�η��̽�Ӧ���⣺
ij�ܵ��ɼס��������̶ӵ���ʩ���ֱ���Ҫ30�졢20��.
��1��������Ӵӹܵ�����ͬʱʩ������Ҫ�������깤��
��2����֪�ӵ���ʩ��ÿ���踶200Ԫʩ���ѣ��Ҷӵ���ʩ��ÿ���踶280Ԫʩ���ѣ���ô���ɼӵ���ʩ�����������Ҷӵ���ʩ��������������ͬʱʩ�������㰴���ٻ�Ǯ����µ�ԭ�����һ����������ͨ������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
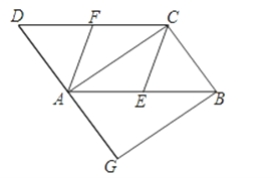
����Ŀ����ͼ����ABCD�У�E��F�ֱ�Ϊ��AB��CD���е㣬AC�ǶԽ��ߣ�����B��BG��AC��DA���ӳ����ڵ�G��
��1����֤��CE��AF��
��2������G=90������֤���ı���CEAF�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������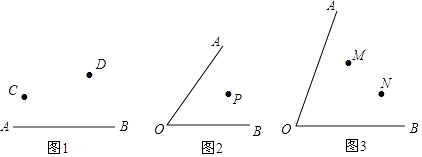
��1����ͼ1����ABֱ��һ��C��D���㣬��AB����һ��P��ʹC��D��P������ɵ������ε��ܳ���̣��ҳ��˵㲢˵�����ɣ�
��2����ͼ2���ڡ�AOB�ڲ���һ��P���Ƿ���OA��OB�Ϸֱ���ڵ�E��F��ʹ��E��F��P������ɵ������ε��ܳ���̣��ҳ�E��F���㣬��˵�����ɣ�
��3����ͼ3���ڡ�AOB�ڲ�������M��N���Ƿ���OA��OB�Ϸֱ���ڵ�E��F��ʹ��E��F��M��N���ĵ���ɵ��ı��ε��ܳ���̣��ҳ�E��F���㣬��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AC��BD�ཻ�ڵ�O����D=��C�����������ĸ��������Բ���ʹ��ADO�ա�BCO���ǣ�������

A. AD=BC B. AC=BD C. OD=OC D. ��ABD=��BAC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ����⣩
��A��B��CΪ���������㣬����C��A�ľ����ǵ�C��B�ľ����2�������ǾͳƵ�C�ǣ�A��B�����ŵ㣮
���磬��ͼ������A��ʾ����Ϊ��1����B��ʾ����Ϊ2����ʾ1�ĵ�C����A�ľ�����2������B�ľ�����1����ô��C�ǣ�A��B�����ŵ㣻���磬��ʾ0�ĵ�D����A�ľ�����1������B�ľ�����2����ô��D�Ͳ��ǣ�A��B�����ŵ㣬����D�ǣ�B��A�����ŵ㣮
��֪ʶ���ã�
��ͼ�ڣ�M��NΪ���������㣬��M����ʾ����Ϊ��2����N����ʾ����Ϊ4��
��1������ ������ʾ�ĵ��ǣ�M��N�����ŵ㣻
��2����ͼ�ۣ�A��BΪ���������㣬��A����ʾ����Ϊ��20����B����ʾ����Ϊ40������һֻ��������P�ӵ�B��������4����λÿ����ٶ������˶��������Aֹͣ����tΪ��ֵʱ��P��A��B��ǡ��һ����Ϊ����������ŵ㣿

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���˶�ʱ��������ͨ�����˵������йء���a��ʾһ���˵����䣬��b��ʾ�����������������˶�ʱ���ܳ��ܵ�ÿ������������ߴ�������![]() .
.

��1����������£�һ��14��������˶�ʱ���ܳ��ܵ�ÿ������������ߴ����Ƕ��٣�
��2����һ���˵���������10��ʱ�����˶�ʱ���ܵ�ÿ����������ߴ����кα仯���仯�����Ƕ��٣�
��3��һ��45������˶�ʱ��10����������Ϊ22�Σ���������Σ����Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCO����ֱ������ϵ�У����ж���B������Ϊ(10�� 8)��E��BC����һ�㽫��ABE��AE�۵�����B�պ���OC���ϵ�D�غϣ�����E�ķ���������y=![]() ��ͼ�����AB���ڵ�F, ���߶�AF�ij�Ϊ( )
��ͼ�����AB���ڵ�F, ���߶�AF�ij�Ϊ( )

A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com