
����Ŀ�����Ķ����⣩
��A��B��CΪ���������㣬����C��A�ľ����ǵ�C��B�ľ����2�������ǾͳƵ�C�ǣ�A��B�����ŵ㣮
���磬��ͼ������A��ʾ����Ϊ��1����B��ʾ����Ϊ2����ʾ1�ĵ�C����A�ľ�����2������B�ľ�����1����ô��C�ǣ�A��B�����ŵ㣻���磬��ʾ0�ĵ�D����A�ľ�����1������B�ľ�����2����ô��D�Ͳ��ǣ�A��B�����ŵ㣬����D�ǣ�B��A�����ŵ㣮
��֪ʶ���ã�
��ͼ�ڣ�M��NΪ���������㣬��M����ʾ����Ϊ��2����N����ʾ����Ϊ4��
��1������ ������ʾ�ĵ��ǣ�M��N�����ŵ㣻
��2����ͼ�ۣ�A��BΪ���������㣬��A����ʾ����Ϊ��20����B����ʾ����Ϊ40������һֻ��������P�ӵ�B��������4����λÿ����ٶ������˶��������Aֹͣ����tΪ��ֵʱ��P��A��B��ǡ��һ����Ϊ����������ŵ㣿

���𰸡���1��2��10����2����tΪ5�롢10���7.5��ʱ��P��A��B��ǡ��һ����Ϊ����������ŵ㣮
��������
��1����������Ϊx�������ŵ�Ķ�����ŵ���M��N֮����ŵ��ڵ�N�ұߣ��г����̽ⷽ�̼��ɣ���2�������ŵ�Ķ����֪�������������PΪ��A��B�����ŵ㣻��PΪ��B��A�����ŵ㣻��BΪ��A��P�����ŵ㣮���P��ʾ����Ϊx�������ŵ�Ķ����г����̣������ó�t��ֵ��
�⣺��1����������Ϊx��
���ŵ���M��N֮��ʱ���������x������2��=2��4��x�������x=2��
���ŵ��ڵ�N�ұ�ʱ���������x������2��=2��x��4������ã�x=10��
�ʴ�Ϊ��2��10��
��2�����P��ʾ����Ϊx����PA=x+20��PB=40��x��AB=40������20��=60��
�����������
��PΪ��A��B�����ŵ㣮
�����⣬��PA=2PB����x������20��=2��40��x����
���x=20��
��t=��40��20����4=5���룩��
��PΪ��B��A�����ŵ㣮
�����⣬��PB=2PA����40��x=2��x+20����
���x=0��
��t=��40��0����4=10���룩��
��BΪ��A��P�����ŵ㣮
�����⣬��AB=2PA����60=2��x+20��
���x=10��
��ʱ����PΪAB���е㣬��AҲΪ��B��P�����ŵ㣬
��t=30��4=7.5���룩��
���Ͽ�֪����tΪ5�롢10���7.5��ʱ��P��A��B��ǡ��һ����Ϊ����������ŵ㣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������� A��B ���㣬����ʾ���������ֱ�Ϊ a��b����֪ AB=12��ԭ�� O ���߶�AB �ϵ�һ�㣬�� OA=2OB.
![]()
��1����a��b��
��2�������� P��Q �ֱ�� A��B ͬʱ�����������˶����� P ���ٶ�Ϊÿ�� 2 ����λ���ȣ��� Q ���ٶ�Ϊÿ�� 1 ����λ���ȣ����˶�ʱ��Ϊ t �룬���� P ��� Q �غ�ʱ��P��Q ����ֹͣ�˶�.
�ٵ� t Ϊ��ֵʱ��2OPOQ=4��
�ڵ��� P ����� O ʱ������ M �ӵ� O ��������ÿ�� 3 ����λ���ȵ��ٶ�Ҳ�����˶������� M �ϵ� Q ���������أ���ͬ�����ٶ���� P �˶��������� P �����������أ���ͬ�����ٶ���� Q �˶������������ֱ���� P��Q ֹͣʱ���� M Ҳֹͣ�˶������ڴ˹����е� M ��ʻ����·�̣���ֱ��д���� M ���λ��������������Ӧ��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ��ѧ��Ϊ�˶�С�����л�������ʶ������ʦ�Ĵ����¶�С���������˲����������������£���ͼ����Ӳ��С�����ز���D��������һ��E�ľ���Ϊ115.2�ף�С�����Ķ���Ϊ��B����BD��DE���ڵ�E����ֱ��һ��ľ�����䶥��ΪC��CE=1.72�ף���DE���ӳ�������һ��A��ʹA��C��B������ͬһֱ���ϣ����AE=4.8�ף���С�����ĸ߶ȣ� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
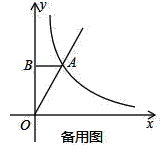
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=kx��˫����![]() �ڵ�һ�����ཻ�ڵ�A��1��2������B��y���ϣ���AB��y�ᣮ��һ����P��ԭ�������y����ÿ��1����λ���ٶ���y����������˶����˶�ʱ��Ϊt�루t��0��������P��PD��y�ᣬ��ֱ��OA�ڵ�C����˫�����ڵ�D��
�ڵ�һ�����ཻ�ڵ�A��1��2������B��y���ϣ���AB��y�ᣮ��һ����P��ԭ�������y����ÿ��1����λ���ٶ���y����������˶����˶�ʱ��Ϊt�루t��0��������P��PD��y�ᣬ��ֱ��OA�ڵ�C����˫�����ڵ�D��
��1����ֱ��y=kx��˫����![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2�����ı���CDAB�����ΪS����P���߶�OB���˶�ʱ��P����B���غϣ�����S��t֮��ĺ�����ϵʽ��
��3����ͼ�е�һ����˫�������Ƿ���ڵ�Q��ʹ��A��B��C��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ������ڣ��������ʱt��ֵ��Q������ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��
��1����A��ʾ����Ϊ ����B��ʾ����Ϊ ����C��ʾ����Ϊ ��
��2���ú�t�Ĵ���ʽ��ʾP����A�͵�C�ľ��룺 PA= ��PC= ��
��3������P�˶���B��ʱ����Q��A���������ÿ��3����λ���ٶ���C���˶���Q�㵽��C�����������ͬ�����ٶȷ��أ��˶����յ�A�����ڵ�Q���C�˶������У��ܷ��ϵ�P?���ܣ��������Q�˶������ϣ����ڵ�Q��ʼ�˶���P��Q����֮��ľ����ܷ�Ϊ2����λ������ܣ��������ʱ��P��ʾ������������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪����A��m��0����B��0��n����n��m��0������C�ڵ�һ���ޣ�AB��BC��BC=BA����P���߶�OB�ϣ�OP=OA��AP���ӳ�����CB���ӳ��߽��ڵ�M��AB��CP���ڵ�N��

��1����C������Ϊ�� ���ú�m��n��ʽ�ӱ�ʾ����
��2����֤��BM=BN��
��3�����C����ֱ��AB�ĶԳƵ�ΪD����C����ֱ��AP�ĶԳƵ�ΪG����֤��D��G����x��Գƣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ຣ������Ѷ��2016��2��21�գ������������̵���ѹ������г�����ϵͳ��ʽ���ã�����������Ͷ����112��Ԫ������40���������г�վ�㡢����720���������г��������������Ͷ�ʣ����ڽ�����վ�㡢���ù������г���Ԥ��2018�꽫Ͷ��340.5��Ԫ���½�120���������г�վ�㡢����2205���������г���
��1������ÿ��վ�����ۺ������г��ĵ��۷ֱ��Ƕ�����Ԫ��
��2���������2016�굽2018�����������ù������г���������ƽ�������ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���У�������
�����ĸ������ǩ�1����|a|=a����a+5һ����a����38���ÿ�ѧ��������ʾΪ38��104��������ʽ��![]() ��ϵ���ǩ�2��������3���ީ�
��ϵ���ǩ�2��������3���ީ�![]() ����
����![]() ����������Ľ����У��������Ķ�������߱��Σ�
����������Ľ����У��������Ķ�������߱��Σ�
A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y��k1x(x��0)��˫����y��![]() (x��0)�ཻ�ڵ�P(2��4)����֪��A(4��0)��B(0��3)������AB����Rt��AOB��OP����ƽ�ƣ�ʹ��O�ƶ�����P���õ���A��PB��.����A����A��C��y�ύ˫�����ڵ�C������CP.
(x��0)�ཻ�ڵ�P(2��4)����֪��A(4��0)��B(0��3)������AB����Rt��AOB��OP����ƽ�ƣ�ʹ��O�ƶ�����P���õ���A��PB��.����A����A��C��y�ύ˫�����ڵ�C������CP.
(1)��k1��k2��ֵ��
(2)��ֱ��PC�Ľ���ʽ��
(3)ֱ��д���߶�ABɨ���������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com