
【题目】)甲乙两人在相同条件下完成了5次射击训练,两人的成绩如图所示.
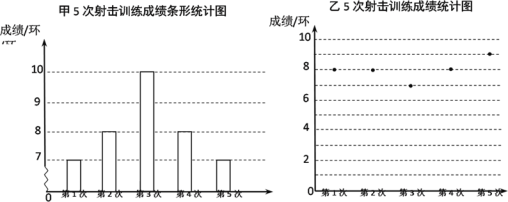
(1)甲射击成绩的众数为 环,乙射击成绩的中位数为 环;
(2)计算两人射击成绩的方差;
(3)根据训练成绩,你认为选派哪一名队员参赛更好,为什么?
【答案】(1)① 7和8 ②8;(2)甲的方差为1.4;乙的方差为0.4;(3)选择乙参赛
【解析】
(1)依据众数、中位数的计算公式,即可得到结果;
(2)根据方差的计算公式进行计算;
(3)依据甲乙两人平均成绩一样,甲射击成绩的方差小于乙,即可得出甲的成绩更加稳定,所以选择甲去参赛.
(1)① 甲5次射击成绩中有两次7环,两次8环,一次10环,所以甲的射击成绩的众数为7和8 ②乙的五次射击成绩从小到大排列为7环,8环,8环,8环,9环,所以乙射击成绩的中位数为8
(2)甲射击成绩的平均数为:![]() ,
,
乙射击成绩的平均数为:![]() =8
=8
S2甲=![]() 1.2,
1.2,
S2乙=![]() =0.4
=0.4
(3)解:∵甲乙二人平均成绩相等,且乙的方差小于甲的方差,
∴选乙参赛更好,因为两人的平均成绩相同,但乙的方差较小,说明乙的成绩更稳定,所以选择乙参赛.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
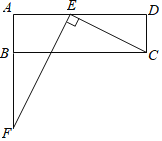
【题目】如图,在矩形ABCD中,已知 AD>AB.在边AD上取点E,连结CE.过点E作EF⊥CE,与边AB的延长线交于点F.
(1)证明:△AEF∽△DCE.
(2)若AB=3,AE =4,AD=10,求线段BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,点P是△ABD的内切圆的圆心,过P作PE⊥BC,PF⊥CD,垂足分别为点E、F,则四边形PECF和矩形ABCD的面积之比等于( )

A.1:2B.2:3C.3:4D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
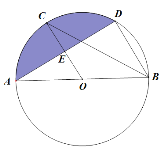
【题目】如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连结BC.
(1)求证:AE=ED;
(2)若AB=8,∠CBD=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.

(1)求反比例函数和一次函数的解析式;
(2)根据图象写出一次函数的值大于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,D,E分别是△ABC两边的中点,如果弧DE(可以是劣弧、优弧或半圆)上的所有点都在△ABC的内部或边上,则称弧DE为△ABC的中内弧.例如,图1中弧DE是△ABC其中的某一条中内弧.
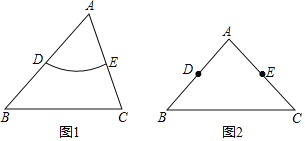
(1)如图2,在边长为4![]() 的等边△ABC中,D,E分别是AB,AC的中点.画出△ABC的最长的中内弧DE,并直接写出此时弧DE的长;
的等边△ABC中,D,E分别是AB,AC的中点.画出△ABC的最长的中内弧DE,并直接写出此时弧DE的长;
(2)在平面直角坐标系中,已知点A(2![]() ,6),B(0,0),C(t,0),在△ABC中,D,E分别是AB,AC的中点.
,6),B(0,0),C(t,0),在△ABC中,D,E分别是AB,AC的中点.
①若t=2![]() ,求△ABC的中内弧DE所在圆的圆心P的纵坐标的取值范围;
,求△ABC的中内弧DE所在圆的圆心P的纵坐标的取值范围;
②请写出一个t的值,使得△ABC的中内弧DE所在圆的圆心P的纵坐标可以取全体实数值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com