
【题目】在△ABC中,D,E分别是△ABC两边的中点,如果弧DE(可以是劣弧、优弧或半圆)上的所有点都在△ABC的内部或边上,则称弧DE为△ABC的中内弧.例如,图1中弧DE是△ABC其中的某一条中内弧.
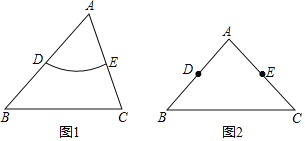
(1)如图2,在边长为4![]() 的等边△ABC中,D,E分别是AB,AC的中点.画出△ABC的最长的中内弧DE,并直接写出此时弧DE的长;
的等边△ABC中,D,E分别是AB,AC的中点.画出△ABC的最长的中内弧DE,并直接写出此时弧DE的长;
(2)在平面直角坐标系中,已知点A(2![]() ,6),B(0,0),C(t,0),在△ABC中,D,E分别是AB,AC的中点.
,6),B(0,0),C(t,0),在△ABC中,D,E分别是AB,AC的中点.
①若t=2![]() ,求△ABC的中内弧DE所在圆的圆心P的纵坐标的取值范围;
,求△ABC的中内弧DE所在圆的圆心P的纵坐标的取值范围;
②请写出一个t的值,使得△ABC的中内弧DE所在圆的圆心P的纵坐标可以取全体实数值.
【答案】(1)图详见解析,![]() ;(2)①m≤
;(2)①m≤![]() 或m≥3;②t=4
或m≥3;②t=4![]() .
.
【解析】
(1)如图1中,由垂径定理可知,圆心O在线段DE的垂直平分线上,当点O是△ABC的内心时,内弧![]() 最长,利用弧长公式计算即可.
最长,利用弧长公式计算即可.
(2)如图2中,由垂径定理可知,圆心一定在线段DE的垂直平分线上,DE的垂直平分线交DE于F,作DO′交DE的垂直平分线于点O′.
①设O′(![]() ,m)由三角形中内弧定义可知,圆心在线段DE上方射线FP上均可,可得m≥3.当O′D⊥OA时,在Rt△DFO′中,∵DF=
,m)由三角形中内弧定义可知,圆心在线段DE上方射线FP上均可,可得m≥3.当O′D⊥OA时,在Rt△DFO′中,∵DF=![]() ,∠FDO′=30°,可得O′F=
,∠FDO′=30°,可得O′F=![]() ,推出O′(
,推出O′(![]() ,
,![]() ),根据三角形中内弧的定义可知,圆心在点O′的下方(含点O′)时也符合要求,可得m≤
),根据三角形中内弧的定义可知,圆心在点O′的下方(含点O′)时也符合要求,可得m≤![]() .
.
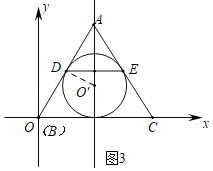
②如图3中,当△AOC是等边三角形时,内弧DE所在圆的圆心P的纵坐标可以取全体实数值.此时t=![]() .
.
解:(1)如图1中,由垂径定理可知,圆心O在线段DE的垂直平分线上,
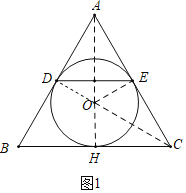
∵△ABC是等边三角形,
∴当点O是△ABC的内心时,内弧![]() 最长,
最长,
在Rt△OHC中,
∵CH=![]() ,∠OCH=30°,
,∠OCH=30°,
∴OH=CHtan30°=2,
∵∠ADE=∠AEO=90°,∠DAE=60°,
∴∠DOE=120°,
∴![]() 的长=
的长=![]() =
=![]() .
.
(2)①如图2中,
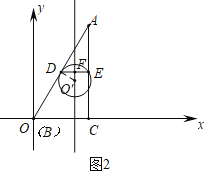
如图2中,由垂径定理可知,圆心一定在线段span>DE的垂直平分线上,DE的垂直平分线交DE于F,
①当t=![]() 时,C(
时,C(![]() ,0),A(
,0),A(![]() ,6),
,6),
∴D(![]() ,3),E(
,3),E(![]() ,6),F(
,6),F(![]() ,3),
,3),
设O′(![]() ,m)由三角形中内弧定义可知,圆心在线段DE上方射线FP上均可,∴m≥3
,m)由三角形中内弧定义可知,圆心在线段DE上方射线FP上均可,∴m≥3
∵tan∠AOC=![]() =
=![]() ,
,
∴∠AOC=60°,
∵DE∥OC,
∴∠ADE=60°,
当O′D⊥OA时,在Rt△DFO′中,∵DF=![]() ,∠FDO′=30°,
,∠FDO′=30°,
∴O′F=![]() ,
,
∴O′(![]() ,
,![]() ),
),
根据三角形中内弧的定义可知,圆心在点O′的下方(含点O′)时也符合要求,
∴m≤![]() ,
,
综上所述,m≤![]() 或m≥3.
或m≥3.
②如图3中,当△AOC是等边三角形时,内弧DE所在圆的圆心P的纵坐标可以取全体实数值.此时t=4![]() .
.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】)甲乙两人在相同条件下完成了5次射击训练,两人的成绩如图所示.
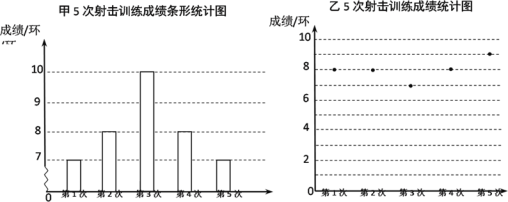
(1)甲射击成绩的众数为 环,乙射击成绩的中位数为 环;
(2)计算两人射击成绩的方差;
(3)根据训练成绩,你认为选派哪一名队员参赛更好,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为2,M、N分别为边BC、CD上的动点,且∠MAN=45°
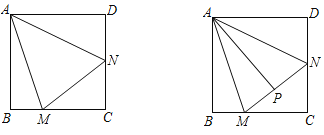
(1)猜想线段BM、DN、MN的数量关系并证明;
(2)若BM=CM,P是MN的中点,求AP的长;
(3)M、N运动过程中,请直接写出△AMN面积的最大值 和最小值 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,过点C作CE⊥DB交DB的延长线于点E,直线AB与CE相交于点F.
(1)求证:CF为⊙O的切线;
(2)填空:当∠CAB的度数为________时,四边形ACFD是菱形.
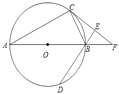
【答案】30°
【解析】(1)连结OC,如图,由于∠A=∠OCA,则根据三角形外角性质得∠BOC=2∠A,而∠ABD=2∠BAC,所以∠ABD=∠BOC,根据平行线的判定得到OC∥BD,再CE⊥BD得到OC⊥CE,然后根据切线的判定定理得CF为⊙O的切线;
(2)根据三角形的内角和得到∠F=30°,根据等腰三角形的性质得到AC=CF,连接AD,根据平行线的性质得到∠DAF=∠F=30°,根据全等三角形的性质得到AD=AC,由菱形的判定定理即可得到结论.
答:
(1)证明:连结OC,如图,
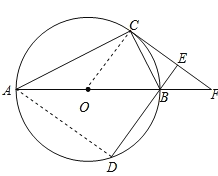
∵OA=OC,
∴∠A=∠OCA,
∴∠BOC=∠A+∠OCA=2∠A,
∵∠ABD=2∠BAC,
∴∠ABD=∠BOC,
∴OC∥BD,
∵CE⊥BD,
∴OC⊥CE,
∴CF为⊙O的切线;
(2)当∠CAB的度数为30°时,四边形ACFD是菱形,理由如下:
∵∠A=30°,
∴∠COF=60°,
∴∠F=30°,
∴∠A=∠F,
∴AC=CF,
连接AD,
∵AB是⊙O的直径,
∴AD⊥BD,
∴AD∥CF,
∴∠DAF=∠F=30°,
在△ACB与△ADB中,
 ,
,
∴△ACB≌△ADB,
∴AD=AC,
∴AD=CF,
∵AD∥CF,
∴四边形ACFD是菱形。
故答案为:30°.
【题型】解答题
【结束】
22
【题目】经市场调查,某种商品在第x天的售价与销量的相关信息如下表;已知该商品的进价为每件30元,设销售该商品每天的利润为y元.

(1)求出y与x的函数关系式
(2)问销售该商品第几天时,当天销售利润最大?最大利润是多少?
(3)该商品销售过程中,共有多少天日销售利润不低于4800元?直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=60°,P为它的内部一点,M为射线OA上一点,连接PM,以P为中心,将线段PM顺时针旋转120°,得到线段PN,并且点N恰好落在射线OB上.
(1)依题意补全图1;
(2)证明:点P一定落在∠AOB的平分线上;
(3)连接OP,如果OP=2![]() ,判断OM+ON的值是否变化,若发生变化,请求出值的变化范围,若不变,请求出值.
,判断OM+ON的值是否变化,若发生变化,请求出值的变化范围,若不变,请求出值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把“有两条边和其中一边的对角对应相等的两个三角形”叫做“同族三角形”,如图1,在△ABC和△ABD中,AB=AB,AC=AD,∠B=∠B,则△ABC和△ABD是“同族三角形”.
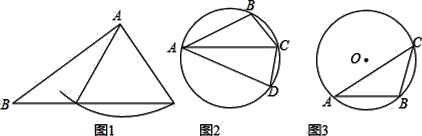
(1)如图2,四边形ABCD内接于圆,点C是弧BD的中点,求证:△ABC和△ACD是同族三角形;
(2)如图3,△ABC内接于⊙O,⊙O的半径为![]() ,AB=6,∠BAC=30°,求AC的长;
,AB=6,∠BAC=30°,求AC的长;
(3)如图3,在(2)的条件下,若点D在⊙O上,△ADC与△ABC是非全等的同族三角形,AD>CD,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=a(x﹣1)(x﹣3)(a<0)的顶点为A,与y轴交于点C,过C作CB∥x轴交抛物线于点B,过点B作直线l⊥x轴,连结OA并延长,交l于点D,连结OB.
(1)当a=﹣2时,求线段OB的长.
(2)是否存在特定的a值,使得△OBD为等腰三角形?若存在,请写出计算过程并求出a的值;若不存在,请说明理由.
(3)设△OBD的外心M的坐标为(m,n),求m与n的数量关系式.
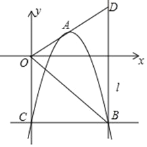
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与x轴交于点
与x轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
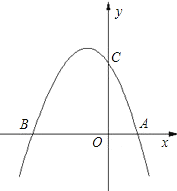
(1)求抛物线的解析式;
(2)若点![]() 为第二象限抛物线上一动点,连接
为第二象限抛物线上一动点,连接![]() ,求
,求![]() 面积的最大值,并求此时
面积的最大值,并求此时![]() 点的坐标.
点的坐标.
(3)在抛物线上是否存在点![]() 使得
使得![]() 为等腰三角形?若存在,请求出一共有几个符合条件的点
为等腰三角形?若存在,请求出一共有几个符合条件的点![]() (简要说明理由)并写出其中一个点的坐标;若不存在这样的点
(简要说明理由)并写出其中一个点的坐标;若不存在这样的点![]() ,请简要说明理由.
,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,∠CAD=20°,则∠DHO的度数是( )
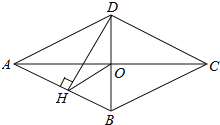
A.20°B.25°C.30°D.40°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com