
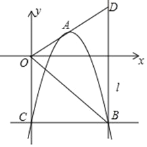
【题目】已知抛物线y=a(x﹣1)(x﹣3)(a<0)的顶点为A,与y轴交于点C,过C作CB∥x轴交抛物线于点B,过点B作直线l⊥x轴,连结OA并延长,交l于点D,连结OB.
(1)当a=﹣2时,求线段OB的长.
(2)是否存在特定的a值,使得△OBD为等腰三角形?若存在,请写出计算过程并求出a的值;若不存在,请说明理由.
(3)设△OBD的外心M的坐标为(m,n),求m与n的数量关系式.
【答案】(1)2![]() (2)a=﹣1或-
(2)a=﹣1或-![]() (3)m=3n2+2
(3)m=3n2+2
【解析】
(1)把a=-2代入y=-2(x-1)(x-3)=-2x2+8x-6,解方程得到点C(0,-6),根据勾股定理即可得到结论;
(2)解方程得到C(0,3a),B(4,3a),过A作AE⊥x轴于点E,AE延长线与CB交于点F,根据三角形的中位线的性质得到DG=2AE=-2a,求得BD=DG+BG=-5a,当△OBD为等腰三角形时,①当OB=BD=-5a,②当OD=BD=-5a时,③当OD=OB时,DG=BG,解方程即可得到结果;
(3)根据已知条件得到点M在BD的垂直平分线上,OM=MD,求得n=![]() a,根据勾股定理列方程即可得到结论.
a,根据勾股定理列方程即可得到结论.
(1)当a=﹣2时,y=﹣2(x﹣1)(x﹣3)=﹣2x2+8x﹣6,
当x=0时,得y=﹣6,
∴点C(0,﹣6),
当y=﹣6时,即﹣6=﹣2x2+8x﹣6,
解得:x=0,或x=4,
∴点B(4,﹣6),
∴BC=4,OC=6,
∴OB═![]() =2
=2![]() ;
;
(2)在y═a(x﹣1)(x﹣3)中,令x═0,得y═3a,
∴C(0,3a),B(4,3a),
∵点A是抛物线的顶点,
∴A(2,-a),
过A作AE⊥x轴于点E,AE延长线与CB交于点F,
将BD与x轴的交点记为点G,
则E为OG的中点,
∵AE∥BD,
∴DG=2AE=﹣2a,
∴BD=DG+BG=﹣5a,
当△OBD为等腰三角形时,分类讨论:
①当OB=BD=﹣5a,在Rt△OBC中,BC=﹣4a=4,
∴a=﹣1,
②当OD=BD=﹣5a时,在Rt△ODG中,25a2﹣4a2=16,
∴a=±![]() ;∵a<0
;∵a<0
∴a=-![]()
③当OD=OB时,DG=BG,但﹣2a≠﹣3a,
∴此种情况不可能;
∴a=﹣1或-![]() ;
;
(3)∵BD=DG+BG=﹣5a,
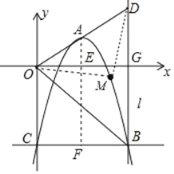
∵点M是△OBD的外心,
∴点M在BD的垂直平分线上,OM=MD,
∴n=![]() a,
a,
∵M(m,n),D(4,﹣2a),
∴(![]() a)2+m2=(﹣
a)2+m2=(﹣![]() a)2+(4﹣m)2,
a)2+(4﹣m)2,
∴8m=6a2+16,
∵n=![]() a,
a,
∴8m=24n2+16,
整理上式,得:m=3n2+2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
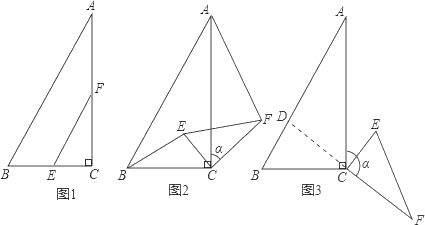
【题目】如图1,在△ABC中,∠ACB=90°,BC=2,∠A=30°,点E,F分别是线段BC,AC的中点,连结EF.
(1)线段BE与AF的位置关系是 ,![]() = .
= .
(2)如图2,当△CEF绕点C顺时针旋转a时(0°<a<180°),连结AF,BE,(1)中的结论是否仍然成立.如果成立,请证明;如果不成立,请说明理由.
(3)如图3,当△CEF绕点C顺时针旋转a时(0°<a<180°),延长FC交AB于点D,如果AD=6﹣2![]() ,求旋转角a的度数.
,求旋转角a的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
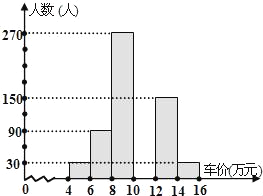
【题目】2007年上海国际汽车展期间,某公司对参观本次车展盛会的且有购车意向的消费者进行了随机问卷调查,共发放900份调查问卷,并收回有效问卷750份.工作人员对有效调查问卷作了统计,其中:
①将消费者年收入的情况整理后,制成表格如下:
年收入(万元) | 4.8 | 6 | 7.2 | 9 | 10 |
被调查的消费者人数(人) | 150 | 338 | 160 | 60 | 42 |
②将消费者打算购买小车的情况整理后,绘制出频数分布直方图(如图,尚未绘完整).(注:每组包含最小值不包含最大值.)请你根据以上信息,回答下列问题:
(1)根据①中信息可知,被调查消费者的年收入的中位数是______万元.
(2)请在图中补全这个频数分布直方图.
(3)打算购买价格10万元以下(不含10万元)小车的消费者人数占被调查消费者人数的百分比是_______.
(4)本次调查的结果,是否能够代表全市所有居民的年收入情况和购车意向?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
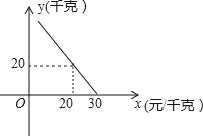
【题目】五家尧草莓是我旗的特色农产品,深受人们的喜欢.某超市对进货价为10元/千克的某种草莓的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)为了让顾客得到实惠,商场将销售价定为多少时,该品种草莓每天销售利润为150元?
(3)应怎样确定销售价,使该品种草莓的每天销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
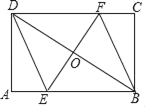
【题目】如图,在矩形ABCD中,AB=8,BC=4,过对角线BD的中点O的直线分别交AB、CD于点E、F,连接DE,BF.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2016年国庆后,许多高校均投放了使用手机就可随用的共享单车.某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费作如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费.具体收费标准如下:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5(含5次以上) |
累计车费 | 0 | 0.5 | 0.9 |
|
| 1.5 |
同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 5 | 15 | 10 | 30 | 25 | 15 |
(Ⅰ)写出![]() 的值;
的值;
(Ⅱ)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利? 说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】武汉素有“首义之区”的美名,2011年9月9日,武汉与台湾将共同纪念辛亥革命一百周年.某校为了了解全校学生对辛亥革命的了解程度,随机抽取了部分学生进行问卷调查,并根据收集的信息进行了统计,绘制了下面尚不完整的统计图. 根据以上的信息,下列判断:①参加问卷调查的学生有50名;②参加进行问卷调查的学生中,“基本了解”的有10人;③扇形图中“基本了解”部分的扇形的圆心角的度数是108°;④在参加进行问卷调查的学生中,“了解”的学生占10%.
其中结论正确的序号是( ).
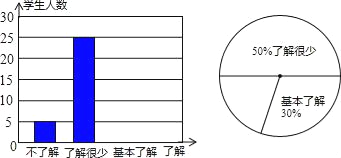
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
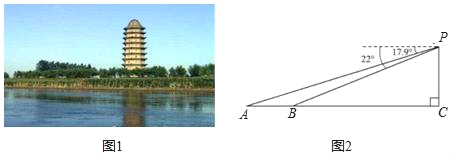
【题目】耸立在临清市城北大运河东岸的舍利宝塔,是“运河四大名塔”之一(如图1).数学兴趣小组的小亮同学在塔上观景点P处,利用测角仪测得运河两岸上的A,B两点的俯角分别为17.9°,22°,并测得塔底点C到点B的距离为142米(A、B、C在同一直线上,如图2),求运河两岸上的A、B两点的距离(精确到1米).(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin17.9°≈0.31,cos17.9°≈0.95,tan17.9°≈0.32)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上.如果BC=4,△ABC的面积是6,那么这个正方形的边长是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com