
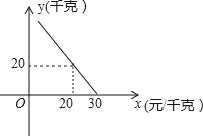
【题目】五家尧草莓是我旗的特色农产品,深受人们的喜欢.某超市对进货价为10元/千克的某种草莓的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)为了让顾客得到实惠,商场将销售价定为多少时,该品种草莓每天销售利润为150元?
(3)应怎样确定销售价,使该品种草莓的每天销售利润最大?最大利润是多少?
【答案】(1)y=﹣2x+60;(2)15元/千克;(3)x=6.5时,利润最大为:245元.
【解析】
(1)把(20,20)、(30,0)代入一次函数y=kx+b,即可求解;
(2)(-20x+60)(x-10)=150,解方程即可;
(3)设售价为x元时,利润W最大,则:w=(-20x+60)(x-10),求函数的最大值即可.
(1)把(20,20)、(30,0)代入一次函数y=kx+b,
解得:k=﹣2,b=60,
函数的表达式为:y=﹣2x+60;
(2)(﹣20x+60)(x﹣10)=150,
解得:x=15或25,
∴为了让顾客得到实惠,商场将销售价定为15时,利润最大;
(3)设售价为x元时,利润W最大,
则:w=(﹣20x+60)(x﹣10)=﹣20(x﹣3)(x﹣10),
当x=10﹣3.5=6.5时,利润最大为:245元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,AB = 6cm,∠CAB = 25°,P是线段AB上一动点,过点P作PM⊥AB交射线AC于点M,连接MB,过点P作PN⊥MB于点N.设A,P两点间的距离为xcm,P,N两点间的距离为ycm.(当点P与点A或点B重合时,y的值均为0)小海根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.

下面是小海的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0.00 | 0.60 | 1.00 | 1.51 | 2.00 | 2.75 | 3.00 | 3.50 | 4.00 | 4.29 | 4.90 | 5.50 | 6.00 |
y/cm | 0.00 | 0.29 | 0.47 | 0.70 | 1.20 | 1.27 | 1.37 | 1.36 | 1.30 | 1.00 | 0.49 | 0.00 |
(说明:补全表格时相关数值保留两位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:当y=0.5时,与之对应的![]() 值的个数是 .
值的个数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(m-1)x2-x-2=0,
(1)若x=-1是方程的一个根,求m的值及另一个根;
(2)当m为何值时方程有两个不同的实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
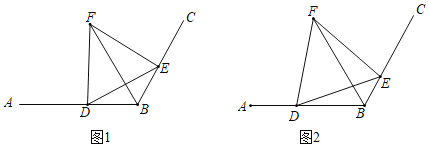
【题目】在图1、2中,已知∠ABC=120°,BD=2,点E为直线BC上的动点,连接DE,以DE为边向上作等边△DEF,使得点F在∠ABC内部,连接BF.
(1)如图1,当BD=BE时,∠EBF= ;
(2)如图2,当BD≠BE时,(1)中的结论是否成立?若成立,请予以证明,若不成立请说明理由;
(3)请直接写出线段BD,BE,BF之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=![]() x2,以D(﹣2,1)为直角顶点作该抛物线的内接Rt△ADB(即A.D.B均在抛物线上).直线AB必经过一定点,则该定点坐标为_____.
x2,以D(﹣2,1)为直角顶点作该抛物线的内接Rt△ADB(即A.D.B均在抛物线上).直线AB必经过一定点,则该定点坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若![]() ,则△A6B6A7的边长为( )
,则△A6B6A7的边长为( )
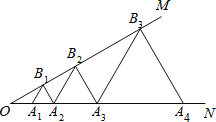
A.6B.12C.16D.32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列分式方程解应用题.
为缓解市区至通州沿线的通勤压力,北京市政府利用既有国铁线路富余能力,通过线路及站台改造,开通了“京通号”城际动车组,每班动车组预定运送乘客1200人,为提高运输效率,“京通号”车组对动车车厢进行了改装,使得每节车厢乘坐的人数比改装前多了![]() ,运送预定数量的乘客所需要的车厢数比改装前减少了4节,求改装后每节车厢可以搭载的乘客人数.
,运送预定数量的乘客所需要的车厢数比改装前减少了4节,求改装后每节车厢可以搭载的乘客人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-4x+3.
(1)在网格中,画出该函数的图象.
(2)(1)中图象与![]() 轴的交点记为A,B,若该图象上存在一点C,且△ABC的面积为3,求点C的坐标.
轴的交点记为A,B,若该图象上存在一点C,且△ABC的面积为3,求点C的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com