
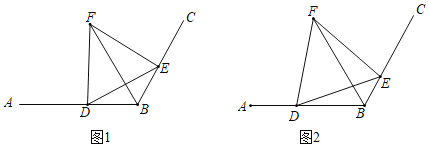
【题目】在图1、2中,已知∠ABC=120°,BD=2,点E为直线BC上的动点,连接DE,以DE为边向上作等边△DEF,使得点F在∠ABC内部,连接BF.
(1)如图1,当BD=BE时,∠EBF= ;
(2)如图2,当BD≠BE时,(1)中的结论是否成立?若成立,请予以证明,若不成立请说明理由;
(3)请直接写出线段BD,BE,BF之间的关系式.
【答案】(1)60°;(2)结论仍然成立,见解析;(3)BF=BD+BE.
【解析】
(1)由“SSS”可证△DBF≌△EBF,可得∠DBF=∠EBF=60°;
(2)如图2,过点F作FG⊥BC,FH⊥AB,由“AAS”可证△FDH≌△FEG,可得FH=FG,由角平分线的性质可得∠ABF=∠FBE=60°;
(3)由全等三角形的性质可得DH=EG,由含30°的直角三角形的性质可得BF=2BH=2BG ,进而可得出BF=BE+BD.
解:(1)∵△DEF是等边三角形,
∴DF=EF=DE,∠DFE=60°,
∵BD=BE,DF=EF,BF=BF,
∴△DBF≌△EBF(SSS)
∴∠DBF=∠EBF,且∠DBF+∠EBF=120°,
∴∠EBF=60°,
故答案为:60°;
(2)结论仍然成立,
理由如下:如图2,过点F作FG⊥BC于点G,,FH⊥AB于点H,
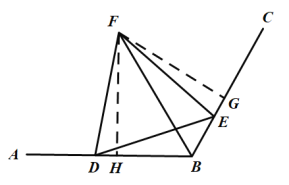
∵△DEF是等边三角形,
∴DF=EF=DE,∠DFE=60°,
∵∠DFE=60°,∠ABC=120°,
∴∠FDB+∠FEB=180°,且∠FEB+∠FEG=180°,
∴∠FDB=∠FEG,且∠FHD=∠FGE=90°,FD=EF,
∴△FDH≌△FEG(AAS)
∴FH=FG,且FG⊥BC,FH⊥AB,
∴∠ABF=∠FBE=60°;
(3)由(2)可知:△FDH≌△FEG,
∴DH=EG,
∴BD+BE=BH+DH+BE=BH+BG,
∵∠ABF=∠FBE=60°,FG⊥BC,FH⊥AB,
∴∠BFH=∠BFG=30°,
∴BF=2BH=2BG,
∴BF=BH+BG=BD+BE.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图,A点的坐标为(﹣1,5),B点的坐标为(3,3),C点的坐标为(5,3),D点的坐 标为(3,﹣1),小明发现:线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BC=EC,∠BCE=∠ACD,如果只添加一个条件,使△ABC ≌ △DEC,则添加的条件不能为( )
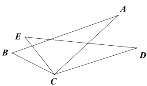
A. ∠B=∠E B. AC=DC C. ∠A=∠D D. AB=DE
查看答案和解析>>
科目:初中数学 来源: 题型:
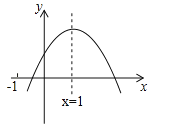
【题目】已知二次函数![]() 的图象如图所示,有以下结论:
的图象如图所示,有以下结论:
①abc>0,
②a﹣b+c<0,
③2a=b,
④4a+2b+c>0,
⑤若点(﹣2,![]() )和(
)和(![]() ,
,![]() )在该图象上,则
)在该图象上,则![]() .
.
其中正确的结论是 (填入正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC和△DEF是两块可完全重合的三角板,![]() ,
,![]() .在如图1所示的状态下,△DEF固定不动,将△ABC沿直线a向左平移.
.在如图1所示的状态下,△DEF固定不动,将△ABC沿直线a向左平移.
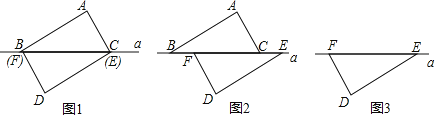
(1)当△ABC移到图2位置时,连解AF、DC,求证:AF=DC;
(2)若EF=8,在上述平移过程中,试猜想点C距点E多远时,线段AD被直线a垂直平分。并证明你的猜想是正确的。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3在坐标系中的位置如图所示,它与x,y轴的交点分别为A,B,P是其对称轴x=1上的动点,根据图中提供的信息,给出以下结论:①2a+b=0,②x=3是ax2+bx+3=0的一个根,③△PAB周长的最小值是![]() +3
+3![]() .其中正确的是( )
.其中正确的是( )
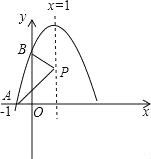
A. ①②③ B. 仅有①② C. 仅有①③ D. 仅有②③
查看答案和解析>>
科目:初中数学 来源: 题型:
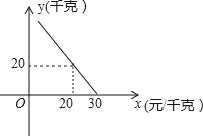
【题目】五家尧草莓是我旗的特色农产品,深受人们的喜欢.某超市对进货价为10元/千克的某种草莓的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)为了让顾客得到实惠,商场将销售价定为多少时,该品种草莓每天销售利润为150元?
(3)应怎样确定销售价,使该品种草莓的每天销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论:①BD平分∠ABC;②AD=BD=BC;③△BDC的周长等于AB+BC;④D是AC中点.其中正确的命题序号是( )

A.①②③ B.①②④ C.②③④ D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
收集数据
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:
甲 78 86 74 81 75 76 87 70 75 90
75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83
80 81 70 81 73 78 82 80 70 40
整理、描述数据
按如下分数段整理、描述这两组样本数据:
成绩 人数 部门 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 0 | 0 | 1 | 11 | 7 | 1 |
乙 |
(说明:成绩80分及以上为生产技能优秀,70--79分为生产技能良好,60--69分为生产技能合格,60分以下为生产技能不合格)
分析数据
两组样本数据的平均数、中位数、众数如下表所示:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | 77.5 | 75 |
乙 | 78 | 80.5 | 81 |